hình đâu

Ta chứng minh BĐT

( a + b + c ) ( 1 a + 1 b + 1 c ) ≥ 9 ( * ) ( * ) < = > 3 + ( a b + b a ) + ( b c + c b ) + ( c a + a c ) ≥ 9

Áp dụng BĐT Cô – si cho hai số dương ta có:

a b + b a ≥ 2 b c + c b ≥ 2 c a + a c ≥ 2 =>(*) đúng

= > 9 a + b + c ≤ 1 a + 1 b + 1 c ≤ 3 = > a + b + c ≥ 3

Trở lại bài toán: Áp dụng BĐT Cô si cho hai số dương ta có  1 + b 2 ≥ 2 b

Ta có: a 1 + b 2 = a − a b 2 1 + b 2 ≥ a − a b 2 2 b = a − a b 2 ( 1 )

Tương tự ta có: 

b 1 + c 2 ≥ b − b c 2 ( 2 ) c 1 + a 2 ≥ c − c a 2 ( 3 )

Cộng từng vế của (1), (2) và (3) ta có:

a 1 + b 2 + b 1 + c 2 + c 1 + a 2 ≥ a + b + c − 1 2 ( a b + b c + c a ) = > a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ a + b + c ≥ 3

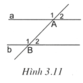
Ta có A 1 ^ + A 2 ^ + B 2 ^ = a ° ⇒ B 2 ^ = a ° − 180 °     (1)

B 1 ^ + B 2 ^ + A 1 ^ = b ° ⇒ A 1 ^ = b ° − 180 °               (2)

Từ (1) và (2), suy ra: B 2 ^ + A 1 ^ = a ° + b ° − 360 ° = 540 ° − 360 ° = 180 ° .

Mặt khác A 2 ^ + A 1 ^ = 180 °  (kề bù) nên B 2 ^ + A 1 ^ = A 2 ^ + A 1 ^ = 180 ° .

Suy ra B 2 ^ = A 2 ^ . Do đó a // b vì có cặp góc đồng vị bằng nhau

a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh

\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu 

Do đó \(\widehat{A_1}=\widehat{B_3}\)

Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù

=> \(\widehat{A_4}=180^0-\widehat{A_1}\)                                  \((1)\)

Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù

=> \(\widehat{B_2}=180^0-\widehat{B_3}\)                                 \((2)\)

\(\widehat{A_1}=\widehat{B_3}\)                                                      \((3)\)

Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)

b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh

\(\widehat{A_4}=\widehat{B_2}\) theo câu a

Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh

\(\widehat{A_1}=\widehat{B_3}\) câu a

Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh

\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)

c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù

\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài

Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)

Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù

\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)

mik chịu thui xin lỗi bạn

xin loi ban minh cung muon giai giup ban lam nhung minh moi hoc lop 5 thoi

mình giống bạn sakura - sorry  nha

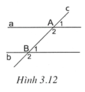
Ÿ Tìm cách giải

Trong hình vẽ đã có những cặp góc đồng vị, cặp góc trong cùng phía. Từ điều kiện trong đề bài, ta có thể suy ra được tổng của hai góc trong cùng phía bù nhau, từ đó suy ra được hai đường thẳng song song.

Ÿ Trình bày lời giải

Ta có A 2 ^ − A 1 ^ = B 2 ^ − B 1 ^ , suy ra A 2 ^ + B 1 ^ = B 2 ^ + A 1 ^ .

Mặt khác A 2 ^ + B 1 ^ + B 2 ^ + A 1 ^ = 360 °  nên A 2 ^ + B 1 ^ = 180 ° .

Suy ra a // b vì có cặp góc trong cùng phía bù nhau