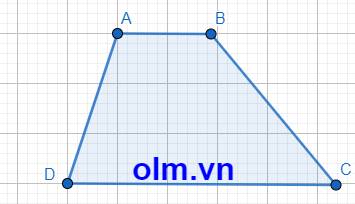
Vì AB//CD nên Góc A và góc D là hai góc trong cùng phía 

          \(\widehat{A}\)+ \(\widehat{D}\) = 180⁰ ⇒ \(\widehat{D}\) + 3\(\widehat{D}\) = 180⁰ ⇒ \(\widehat{D}\) = 180⁰:4 = 45⁰

          \(\widehat{A}\) = 45⁰.3 =135⁰

           \(\widehat{B}\)+\(\widehat{C}\) = 180⁰ ⇒ \(\widehat{B}\) + \(\widehat{B}\) - 30⁰ = 180⁰ ⇒2\(\widehat{B}\) =210⁰ ⇒ \(\widehat{B}\) = 105⁰

           \(\widehat{C}\) = 105⁰ - 30⁰ = 75⁰

a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.

Vì AB//CD, ta có góc ACD = góc BAD.

Vậy số đo góc A là 120 độ.

b) Gọi góc BCD là x độ.

Theo giả thiết, góc B phần góc D = 4/5, ta có:

góc B = (4/5) * góc D

= (4/5) * 60

= 48 độ.

Vì AB//CD, ta có góc BCD = góc BAD.

Vậy góc BAD = góc BCD = x độ.

Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.

Ta có: góc A + góc B + góc C + góc D = 360 độ.

Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:

120 + 48 + góc C + 60 = 360

góc C = 360 - 120 - 48 - 60 = 132 độ.

Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.

* Ib = bài 4

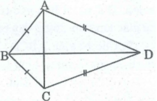
Xét ∆ BAD và  ∆ BCD, ta có:

BA = BC (gt)

DA = DC (gt)

BD cạnh chung

Suy ra:  ∆ BAD =  ∆ BCD (c.c.c)

⇒  ∠ (BAD) = ∠ (BCD)

Mặt khác, ta có:  ∠ (BAD) +  ∠ (BCD) +  ∠ (ABC) +  ∠ (ADC) = 360 0

Suy ra:  ∠ (BAD) +  ∠ (BCD) =  360 0  – ( ∠ (ABC) +  ∠ (ADC) )

2 ∠ (BAD) =  360 0 - 100 0 + 70 0 = 190 .

⇒  ∠ (BAD) = 190 0 : 2 = 95 0

⇒  ∠ (BCD) =  ∠ (BAD) =  95 0

Ta có AB // CD

\(\Rightarrow\)\(\widehat{A}+\widehat{D}=180\)

Mà \(\widehat{A}-\widehat{D}=20\)( gt )

\(\Rightarrow\)\(\widehat{A}=\left(180+20\right):2=100\)

\(\widehat{D}=100-20=80\)

\(\widehat{B}+\widehat{C}=180\)  ( tcp ; AB // CD )

Mà \(\widehat{B}=2\widehat{C}\)    ( gt )

\(\Rightarrow\)\(2\widehat{C}+\widehat{C}=180\)

\(\Rightarrow\)\(3.\widehat{C}=180\)

             \(\widehat{C}=180:3=60\) 

\(\Rightarrow\)\(\widehat{B}=60.2=120\)

Vậy ...............................................

Mình không biết bài này 

b1  a) goi I la giao diem cua AD va BC

vi AB//DC => goc IDC = goc DAB (2 goc dong vi)

ma goc A =30  => goc IDC =30

lai co  goc IDC + goc ADC =180 ( I,D,A thang hang)

                                                     30+ goc ADC =180 => goc ADC=150

vi AB//DC => goc ICD = goc CBA (2 goc dong vi)

có goc ICD+ goc DCB =180 (I,C,B thang hang )

goc ICD+ 120=180   => goc ICD = 60 => goc ABC=60

còn ý b) bạn làm tương tự nhé

b2

vi DC =BC (gt) => tam giac DCB can tai C  => goc CDB = goc DBC (1)

vi DB la phan giac cua goc ADC => g ADB =g BDC  (2)

tu (1,2) => g ADB = g DBC

ma 2 goc nay o vi tri so le trong

=> AD// BC  => ABCD la hinh thang

bài 2:

Ta có: DC = BC

   => Góc CDB = góc CBD ( quan hệ giữa góc và cạnh đối diện)

  Mà góc ADB = góc CDB ( gt)

   => Góc ADB = góc CBD

  Mà 2 góc này ở vị trí so le trong => AB //CD

   => ABCD là hình thang

Bài 3:

  a)  xét tam giác BEC và tam giác CDB có:

           Góc CEB = góc BDC = 90 độ

           BC là cạnh chung

           Góc B = góc C ( tam giác ABC cân tại A)

       => Tam giác BEC = tam giác CDB ( ch-cgv)

       => BE = DC ( 2 cạnh tương ứng)

       => BD = CE (  2 cạnh tương ứng )   

    b) Ta có:  AE + EB = AB

                   AD + DC = AC

             Mà EB = DC ( CMT)

                   AB = AC ( tam giác ABC cân tại A)

          => AE = AD

     c) Ta có: AE = AD => tam giác AED cân tại A

            => góc AED = góc ADE = \(\frac{180-A}{2}\)(1)

         Ta có tam giác ABC cân tại A

            => góc B = góc C =\(\frac{180-A}{2}\)        (2)

   Từ (1) và(2) => góc AED = góc B 

            Mà 2 góc này ở vị trí đồng vị=> ED//BC=> BEDC là hình thang