làm giúp mình đi mà 

Ve hinh di

ái chà

a/ . Gọi S là diện tích:

Ta có:

SBAHE = 2 SCEH

Vì BE = EC và hai tam giác BHE, HEC có cùng chiều cao hạ từ đỉnh chung H nên S(BHE) = S(HEC)

Do đó S(BAH)= S(BHE) = S(HEC)

Suy ra: S(ABC) = 3 S(BHA) và AC = 3 HA ( vì hai tam giác ABC và BHA có cùng chiều cao hạ từ đỉnh chung B)

Vậy HA = AC : 3 = 6 : 3 = 2 ( cm)

Nghĩa là điểm H phải tìm cách A là 2cm

b/ Ta có: S(ABC) = 6 x 3 : 2 = 9 ( cm2)

 Vì BE = EC và hai tam giác BAE, EAC có cùng chiều cao hạ từ đỉnh chung A, nên S(BAE) = S(EAC) do đó:

S(EAC) = 0,5      S(ABC) = 9 : 2 = 4,5 (cm2)

    Vì S(HEC) = 1/3 S(ABC) = 9 : 3 = 3 (cm2)

Nên S(AHE)= 4,5 – 3 = 1,5 (cm2)

a)

Ta có: S_BAHE = 2 S_CEH

Và S_BHE = S_HEC  (BE=EC, chung đường cao kẻ từ H).

Do đó S_BAH= S_BHE = S_HEC   (1)

Suy ra S_ABC = 3S_BHA. Mà hai tam giác ABC và BHA có chung đường cao kẻ từ B.

Nên HA = AC/3 = 6 : 3 = 2 ( cm).

b)

Ta lại có: S_ABC = 6 x 3 : 2 = 9 ( cm²).

S_EAC = 1/2S_ABC = 9 : 2 = 4,5 (cm²) (EC = ½ BC, chung đường cao kẻ từ A).

Từ (1) cho ta: S_EHC = 9 : 3 =  3 (cm²)

Mà:  S_AEH = S_AEC – S_EHC = 4,5 – 3 = 1,5 (cm²)

Câu hỏi là gì vậy ?

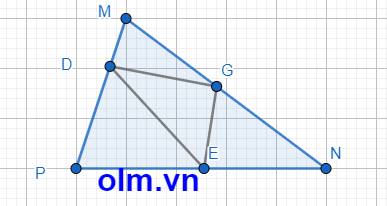
Tỉ số diện tích tam giác PDE và diện tích tứ giác DMNE  là:

                         1 : 2 = \(\dfrac{1}{2}\)

Ta có sơ đồ: 

Theo sơ đồ ta có: Diện tích tam giác BDE  = 360 : (1+2) = 120 (cm²)

 Diện tích tứ giác DMNE là: 360 - 120 = 240 (cm²)

  S_MEP = \(\dfrac{1}{2}\)S_MNP vì ( hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy PN và PE = \(\dfrac{1}{2}\) PN)

S_MEP = 360 \(\times\) \(\dfrac{1}{2}\)  = 180(cm²)

Tỉ số diện tích S_DEP và S_MEP  là:  120 : 180 = \(\dfrac{2}{3}\) ⇒ PD = \(\dfrac{2}{3}\) PM ( vì hai tam giác có chung đường cao hạ từ đỉnh E xuống đáy PM nên tỉ số diện tích hai tam giác là tỉ số của hai cạnh đáy)

Cạnh MD bằng: 1 - \(\dfrac{2}{3}\) = \(\dfrac{1}{3}\) (cạnh PM) 

S_MGD = \(\dfrac{1}{3}\) S_MGP ( Vì hai tam giác có chung đường cao hạ từ đỉnh G xuống đáy PM và MD = \(\dfrac{1}{3}\) PM)

S_MGP = \(\dfrac{1}{2}\) S_MNP ( Vì hai tam giác có chung đường cao hạ từ đỉnh P xuống đáy MN và MG = \(\dfrac{1}{2}\) MN)

⇒ S_MGP = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{2}\) S_MNP = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{2}\) \(\times\) 360 = 60 (cm²)

S_GEN = \(\dfrac{1}{2}\)S_GPN ( vì hai tam giác có chung đường cao hạ từ đỉnh G xuông đáy PN và EN = \(\dfrac{1}{2}\)PN)

Tương tự ta có: S_GPN  = \(\dfrac{1}{2}\) S_MNP  

⇒ S_GEN = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{1}{2}\) \(\times\) 360 = 90 (cm²)

S_GDE = S_MNED - S_MGD - S_GEN = 240 - 60 -90 =  90 (cm²)

Đáp số: 90 cm²