Hai bán kính OA, OB của đường tròn (O; R) tạo với nhau một góc 750 thì độ dài cung nhỏ AB là:
A. \(\frac{3\pi R}{4}\)
B. \(\frac{5\pi R}{12}\)
C. \(\frac{7\pi R}{24}\)
D. \(\frac{4\pi R}{5}\)
Những câu hỏi liên quan
Cho hai hình tròn đồng tâm O,bán kính OB1cm,BA1cm.Tính hiệu của:a)Chu vi hình tròn OA và chu vi hình tròn OB.b)Diện tích hình tròn bán kính OA và diện tích hình tròn bán kinh OBDựa vào kết quả bài trên hãy tìm tỉ số phần trăm của:a)Chu vi hình tròn bán kính OB và chu vi hình tròn bán kính OAb)Diện tích hình tròn bán kính OB và diện tích hình tròn bán kính OAgiúp mik nha mik đang cần gấp
Đọc tiếp
Cho hai hình tròn đồng tâm O,bán kính OB=1cm,BA=1cm.Tính hiệu của:
a)Chu vi hình tròn OA và chu vi hình tròn OB.
b)Diện tích hình tròn bán kính OA và diện tích hình tròn bán kinh OB
Dựa vào kết quả bài trên hãy tìm tỉ số phần trăm của:
a)Chu vi hình tròn bán kính OB và chu vi hình tròn bán kính OA
b)Diện tích hình tròn bán kính OB và diện tích hình tròn bán kính OA
giúp mik nha mik đang cần gấp
Cho A, B nằm cùng trong mặt phẳng của đường tròn O bán kính 5 cm.Biết OA + OB + BC = 15 (cm); OB - OA = 1 ( cm );
OB - AB = 5 (cm). Chứng minh A và B nằm ngoài đường tròn O bán kính 5 cm
Cho đường tròn tâm O, bán kính R=3 cm và hai điểm A,B nằm trên đường tròn (O) sao cho số đo cung lớn bằng 240°. Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OB vsf cung nhỏ AB.
Cho đường tròn (O) bán kính OA và đường tròn (O') đường kính OA. Vị trí tương đối của hai đường tròn là:
A. Nằm ngoài nhau
B. Cắt nhau
C. Tiếp xúc ngoài
D. Tiếp xúc trong
Chọn đáp án D
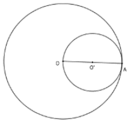
Vì hai đường tròn có một điểm chung là A và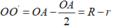 
nên hai đường tròn tiếp xúc trong
Đúng 0
Bình luận (0)
Cho đường tròn (O) bán kính OA và đường tròn (O') đường kính OA. Vị trí tương đối của hai đường tròn là:
A. Nằm ngoài nhau
B. Không giao nhau
C. Cắt nhau
D. Tiếp xúc
Đáp án D
Hai đường tròn có một điểm chung là A nên hai đường tròn tiếp xúc nhau.
Đúng 0
Bình luận (0)
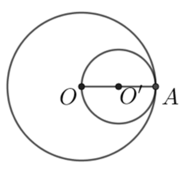
Cho đường trong (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC ^ OA. Biết độ dài đường tròn (O) 4π cm. Tính:
a, Bán kính đường tròn (O)
b, Độ dài hai cung BC của đường tròn
a, 2πR = 4π => R = 2cm
b, A O B ^ = 60 0 (DOAB đều)
=> B O C ^ = 120 0
l B C ⏜ n h ỏ = π . R . 120 180 = 4 π 3 cm
và l B C ⏜ l ớ n = 8 3 π cm
Đúng 1
Bình luận (0)
8 tháng 10 2023 lúc 7:36
Cho đường tròn (O; R). Qua điểm A thuộc đường tròn, kẻ tiếp tuyến Ax, trên đó lấy điểm B sao cho \(OB=\sqrt{2}R\), OB cắt đường tròn (O) ở C.
a) Tính số đo góc ở tâm tạo bởi hai bán kính OA, OC;
b) Tính số đo các cung AC của đường tròn (O).
a: Xét ΔBAO vuông tại A có \(cosAOB=\dfrac{OA}{OB}=\dfrac{1}{\sqrt{2}}\)
=>\(\widehat{AOC}=45^0\)
=>\(sđ\left(OA;OC\right)=45^0\)
b: Số đo cung AC nhỏ là:
\(sđ\stackrel\frown{AC}=45^0\)
Số đo cung AC lớn là:
3600-450=3150
Đúng 1
Bình luận (0)
Cho đường tròn (O), bán kính OA bằng $\sqrt5 cm$. Kẻ bán kính OB vuông góc với OA. Gọi I là trung điểm của OB. Vẽ dây AC đi qua I. Tính độ dài AC.
Xem thêm câu trả lời
Cho xOy. Trên 2 cạnh Ox và Oy người ta lấy 2 điểm A,B sao cho OA=OB. Dựng đường tròn tâm A, bán kính OA và đường tròn tâm B, bán kính OB. Hai đường tròn này cắt nhau tại điểm thứ 2 là I. C.minh tia OI là phân giác của xOy
Xét ΔOAI và ΔOBI có
OA=OB
OI chung
AI=BI
Do đó: ΔOAI=ΔOBI
Suy ra: \(\widehat{AOI}=\widehat{BOI}\)
hay OI là tia phân giác của góc xOy
Đúng 0
Bình luận (0)
cho đường tròn (O,R ) qua điểm A thuộc đường tròn , kẻ tiếp tuyến Ax trên đó lấy điểm B sao cho OB=căn hai R , OB cắt đường tròn (o) ở C a, tính sao đo góc ở tâm tạo bởi 2 bán kính OA, OC b, tính số đo các cung AC cửa đường tròn (O)
Good luck~