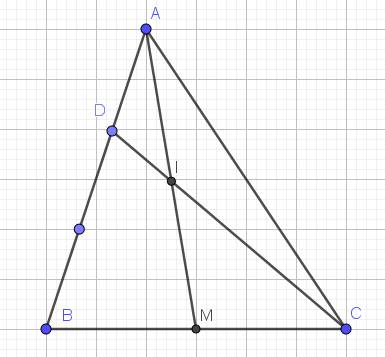
Cho tam giác ABC .Gọi M là trung điểm BC ,I là trung điểm AM ,D là giao điểm của CI và AB . C/m AD= 1/2DB

Những câu hỏi liên quan
Cho tam giác ABC. Gọi M là trung điểm của BC, I là trung điểm của AM,
D là giao điểm của CI và AB. CMR:AD = 1/2DB.
cho tam giác abc
m là trung điểm bc
i là trung điểm am
ci giao ab tại d
cmr : ad=1/2db
cho tam giác ABC trung tuyến AM. Gọi I là trung điểm của AM, D là giao điểm của CI và AB. C/m AD = 1/2 BD
Cho tam giác ABC gọi M là trung điểm của BC , I là trung điểm của AM , D là giao điểm của CI và AB . Chứng minh rằng AD = 1/2 DB
dùng t/c 3 đường trung tuyến tam giác nhé!!
54365465
Đúng 0
Bình luận (0)
a) Xet tam giac ADE va tam giac FEC ta co:
AE=EC ( E la trung diem AC )
DE= EF ( E la trung diem DF)
goc AED= goc CEF ( 2 goc doi dinh )
==> tam giac ADE = tam giac FEC ( c=g=c)
---> AD= CF ( 2 canh tuong ung )
ma AD=DB ( D la trung diem AB)
nen DB=CF
b) ta co: goc EAD = goc ECF ( tam gia ADE= tam giac FEC)
ma goc EAD va goc ECF nam o vi tri so le trong
nen AD// CF hay AB// CF
xet tam giac BDC va tam giac DCF ta co:
BD= CF ( cm a)
DC=DC ( canh chung)
goc BDC= goc FCD (2 goc so le trong va AB//CF)
--> tam giac BDC= tam giac DCF ( c=g=c)
c) ta co :
DE=1/2 DF ( E la trung diem DF)
DF= BC ( tam giac FCD= tam giac BDC)
--> DE=1/2 BC
Đúng 0
Bình luận (0)
Cho tam giác ABC, gọi M là trung điểm BC, I là trung điểm AM, D là giao điểm của CI và AB. Chứng minh rằng AD = 1/2 DB
Từ điểm M kẻ đường thẳng Mx song song với DC cắt AB tại H
xét tam giác AHM có : DI // HM (DC // Mx)
AI = IM (gt)
=> DI là đường trung bình của tam giác AHM
=> AD =DH (1)
xét tam giác BDC có: DC // HM (DC // Mx)
BM = MC (gt)
=> HM là đường trung bình của tam giác BDC
=> DH = HB (2)
từ (1) và (2) => AD = DH = HB
=> AD=1/2 DB
=> đpcm
Chúc bạn học tốt
từ điểm M kẻ đường thẳng mx song song với DC cắt AB tại H
xét tam giác AHM có : DI song song HM ( DC song song Mx )
AI=IM (gt)
suy ra DI là đường trung bình của tam giá AHM
suy ra AD= DH (1)
xét tam giác BDC có: DC song song HM( DC song song Mx )
BM = MC (gt)
suy ra HM là đường trung bình của tam giác BDC
suy ra DH =HB (2)
TỪ (1) VÀ (2) suy ra AD =DH =HB
suy ra AD=1/2 DB HAY BD =2AD
suy ra đpcm
cho tam giác ABC
gọi M là trung điểm Bc
I là trung điểm AM
D là giao điểm của CI và AB
CMR : AD = 1/2 DB
Tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. K là trung điểm DB. D là giao điểm của CI và AB. Chứng minh AD = 1/2 DB
Cho tam giác ABC có M là trung điểm của BC. Lấy điểm D trên cạnh AB sao cho BD=2AD. Gọi I là giao điểm của CD và AM. CMR I là trung điểm của AM và CI=3DI
Lời giải:
Áp dụng định lý Menelaus cho tam giác $ABM$ và $D,I,C$ thẳng hàng:
$\frac{AD}{DB}.\frac{IM}{IA}.\frac{CB}{CM}=1$
$\Rightarrow \frac{1}{2}.\frac{IM}{IA}.2=1$
$\Rightarrow \frac{IM}{IA}=1\Rightarrow IM=IA$ hay $I$ là trung điểm của $AM$.
Tiếp tục áp dụng định lý Menelaus cho tam giác $CBD$ có $I,A,M$ thẳng hàng:
$\frac{MC}{MB}.\frac{ID}{IC}.\frac{AB}{AD}=1$
$\Rightarrow 1.\frac{ID}{IC}.3=1$
$\Rightarrow \frac{ID}{IC}=\frac{1}{3}\Rightarrow CI=3DI$
Đúng 1
Bình luận (0)
Cho tam giác ABC gọi M là trung điểm của BC , I là trung điểm của AM , D là giao điểm của CI và AB . Chứng minh rằng AD = 1/2 DB
a) Xet tam giac ADE va tam giac FEC ta co:
AE=EC ( E la trung diem AC )
DE= EF ( E la trung diem DF)
goc AED= goc CEF ( 2 goc doi dinh )
==> tam giac ADE = tam giac FEC ( c=g=c)
---> AD= CF ( 2 canh tuong ung )
ma AD=DB ( D la trung diem AB)
nen DB=CF
b) ta co: goc EAD = goc ECF ( tam gia ADE= tam giac FEC)
ma goc EAD va goc ECF nam o vi tri so le trong
nen AD// CF hay AB// CF
xet tam giac BDC va tam giac DCF ta co:
BD= CF ( cm a)
DC=DC ( canh chung)
goc BDC= goc FCD (2 goc so le trong va AB//CF)
--> tam giac BDC= tam giac DCF ( c=g=c)
c) ta co :
DE=1/2 DF ( E la trung diem DF)
DF= BC ( tam giac FCD= tam giac BDC)
--> DE=1/2 BC
mình nha mình lại cho
Đúng 0
Bình luận (0)
a) Xet tam giac ADE va tam giac FEC ta co:
AE=EC ( E la trung diem AC )
DE= EF ( E la trung diem DF)
goc AED= goc CEF ( 2 goc doi dinh )
==> tam giac ADE = tam giac FEC ( c=g=c)
---> AD= CF ( 2 canh tuong ung )
ma AD=DB ( D la trung diem AB)
nen DB=CF
b) ta co: goc EAD = goc ECF ( tam gia ADE= tam giac FEC)
ma goc EAD va goc ECF nam o vi tri so le trong
nen AD// CF hay AB// CF
xet tam giac BDC va tam giac DCF ta co:
BD= CF ( cm a)
DC=DC ( canh chung)
goc BDC= goc FCD (2 goc so le trong va AB//CF)
--> tam giac BDC= tam giac DCF ( c=g=c)
c) ta co :
DE=1/2 DF ( E la trung diem DF)
DF= BC ( tam giac FCD= tam giac BDC)
--> DE=1/2 BC
Đúng 0
Bình luận (0)