bn co sai de ai khong z

Thay x=-5 vào (d1), ta được:

\(y=\dfrac{1}{5}\cdot\left(-5\right)+1=-1+1=0\)

Vì (d2)//(d3) nên \(\left\{{}\begin{matrix}a=-\dfrac{2}{5}\\b\ne-11\end{matrix}\right.\)

Vậy: (d2): \(y=-\dfrac{2}{5}x+b\)

Thay x=-5 và y=0 vào (d2), ta được:

\(b-\dfrac{2}{5}\cdot\left(-5\right)=0\)

=>b+2=0

=>b=-2

Vậy: (d2): \(y=-\dfrac{2}{5}x-2\)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{5}\cdot0+1=1\end{matrix}\right.\)

Tọa độ C là:

\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{2}{5}\cdot0-2=-2\end{matrix}\right.\)

Vậy: A(-5;0); B(0;1); C(0;-2)

\(AB=\sqrt{\left(0+5\right)^2+\left(1-0\right)^2}=\sqrt{26}\)

\(AC=\sqrt{\left(0+5\right)^2+\left(-2-0\right)^2}=\sqrt{29}\)

\(BC=\sqrt{\left(0-0\right)^2+\left(-2-1\right)^2}=3\)

Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{26+29-9}{2\cdot\sqrt{26}\cdot\sqrt{29}}=\dfrac{23}{\sqrt{754}}\)

=>\(sinBAC=\sqrt{1-\left(\dfrac{23}{\sqrt{754}}\right)^2}=\dfrac{15}{\sqrt{754}}\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)

\(=\dfrac{1}{2}\cdot\dfrac{15}{\sqrt{754}}\cdot\sqrt{26\cdot29}=7,5\)

a, cắt : a khác a'
b, b= b'; a khác a'
c, a=a' ; b khác b'
d, a*a'= -1
e, a= a' ;b= b'

Hai đường thẳng ( d 1 ) và ( d 2 ) cắt nhau tại M(2; -5) nên:

M ∈ ( d 1  ): 3 a - 1 2 + 2b.(-5) = 56 ⇔ 6a - 10b = 58

Khi đó, ta có hệ phương trình:

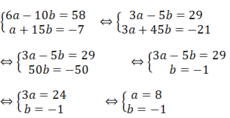
Vậy a = 8 và b = -1 thì hai đường thẳng ( d 1  ) và ( d 2  ) cắt nhau tại M(2; -5).

\(PTHDGD:mx-m+2=\left(m-3\right)x+m\\ \text{Thay }x=0\Leftrightarrow2-m=m\Leftrightarrow m=1\)