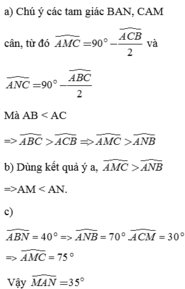cho \(\Delta\)ABC biết A^ = 600, B^ =700 tính góc C so sánh AC và BC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, góc B có số đo bằng 600 . Vẽ AH vuông góc với BC, (H ∈ BC ) a. So sánh AB và AC; BH và HC; b. Lấy điểm D thuộc tia đối của tia HA sao cho HD = HA. Chứng minh rằng hai tam giác AHC và DHC bằng nhau. c. Tính số đo của góc BDC.
Cho tam giác ABC có góc A tù, AB AC. Trên cạnh BC lấy M và N sao cho BN BA, CM CA.a) So sánh
A
M
C
^
và
A
N
B
^
.b) So sánh AM và AN.c) Cho biết
A
B
C
^
40
°
,
A...
Đọc tiếp
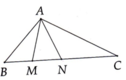
Cho tam giác ABC có góc A tù, AB < AC. Trên cạnh BC lấy M và N sao cho BN = BA, CM = CA.
a) So sánh A M C ^ và A N B ^ .
b) So sánh AM và AN.
c) Cho biết A B C ^ = 40 ° , A C B ^ = 30 ° .Tính ba góc tam giác AMN.
Cho \(\Delta ABC\)vuông tại A .M là TĐ của AC .Trên tia đối tia MB lấy điểm E sao ME=MB.CMR
a)\(\Delta AMB=\Delta CME\)
B) So sánh CE và BC
c) So sánh góc BAM và góc MBC
d)CMR;AE//BC
GIÚP MÌNH VỚI CÁC BẠN ƠI
1) Cho Delta MNP(MNMP), MI là đường phân giác của Delta MNPa. So sánh IN và IPb. Trên tia đối của tia IM lấy điểm A. SO sánh NA và PA.2) Cho Delta ABCvuông ở A (ABAC) có AH là đường cao. So sánh AH+BC và AB+AC.3) CHo Delta ABCcó góc A80 độ, góc B70 độ, AD là đường phân giác của Delta ABCa. CM: CDABb. Vẽ BH vuông góc với AD (H thuộc AD). CMR: CD2BH4) CHo Delta ABCnhọn, các đường trung tuyến BD, CE vuông góc với nhau. Giả sử AB6cm, AC8cm. Tính độ dài BC?5) Cho Delta ABCcó đường cao AH (H nằm giữa...
Đọc tiếp
1) Cho \(\Delta MNP\)(MN<MP), MI là đường phân giác của \(\Delta MNP\)
a. So sánh IN và IP
b. Trên tia đối của tia IM lấy điểm A. SO sánh NA và PA.
2) Cho \(\Delta ABC\)vuông ở A (AB<AC) có AH là đường cao. So sánh AH+BC và AB+AC.
3) CHo \(\Delta ABC\)có góc A=80 độ, góc B=70 độ, AD là đường phân giác của \(\Delta ABC\)
a. CM: CD>AB
b. Vẽ BH vuông góc với AD (H thuộc AD). CMR: CD=2BH
4) CHo \(\Delta ABC\)nhọn, các đường trung tuyến BD, CE vuông góc với nhau. Giả sử AB=6cm, AC=8cm. Tính độ dài BC?
5) Cho \(\Delta ABC\)có đường cao AH (H nằm giữa B và C). CMR
a. Nếu \(\frac{AH}{BH}=\frac{CH}{AH}\)thì \(\Delta ABC\)vuông
b. Nếu \(\frac{AB}{BH}=\frac{BC}{AB}\)thì \(\Delta ABC\)vuông
c. Nếu \(\frac{AB}{AH}=\frac{BC}{AC}\)thì \(\Delta ABC\)vuông
d. Nếu \(\frac{1}{AH^2}=\frac{1}{AB^2}=\frac{1}{AC^2}\)thì \(\Delta ABC\)vuông
Cho ∆ABC vuông tại A(AB lớn hơn AC. a,so sánh góc b và c,tính AB biết BC=10cm, AC 6cm
b,Trên cạnh BC lấy điểm D sao cho BD bằng AB.Đườnh thẳng vuông góc với BC tại D cắt AC ở E.CM ∆ABE bằng ∆DBE và AE nhỏ hơn CE
Xem chi tiết
cho tam giác ABC có góc A =60o , AB<AC đường cao BH ( H thuộc AC).
a) so sánh góc ABC và góc ACB . Tính góc ABH.
b) vẽ AD là phân giác góc A ( A thuộc BC) , vẽ BI vuông góc với AD tại I . Chứng minh \(\Delta\)AIB=\(\Delta\)BHA
c) Tia BI cắt AC tại E . Chứng minh \(\Delta\)ABE đều
d) chứng minh DC>DB
a ) Ta có :
+) \(AB< AC\) ( gt )
\(\Rightarrow ACB< ABC\) ( quan hệ gữa góc và cạnh đối diện )
+ ) \(ABH+BAH+AHB=180\)( tổng ba góc trong một tam giác )
\(\Rightarrow ABH+60+90=180\)
\(\Rightarrow ABH=30\)
b ) Ta có :\(AD\)là phân giác góc \(A\) ( gt )
\(\Rightarrow BAD=CAD=\frac{BAC}{2}=\frac{60}{2}=30\)
Mà \(ABH=30\) ( cmt )
\(\Rightarrow ABH=BAD\)
\(\Rightarrow ABH=BAI\)
Xét tam giác \(AIB\) và tam giác \(BHA\) có :
\(AB\) chung
\(AIB=BHA=90\)
\(BAI=ABH\)
\(\Rightarrow\) tam giác \(AIB\) \(=\) tam giác \(BHA\) ( g - c - g )
c ) Xét tam giác \(ABI\) có :
\(ABI+BAI+AIB=180\)( tổng ba góc trong một tam giác )
\(\Rightarrow ABI+30+90=180\)
\(\Rightarrow ABI=60\)
\(\Rightarrow ABE=60\) ( 1 )
Xét tam giác \(ABE\) có :
\(ABE+BAE+AEB=180\) ( tổng ba góc trong một tam giác )
\(\Rightarrow60+60+AEB=180\)
\(\Rightarrow AEB=60\) ( 2 )
Mà \(BAE=60\) ( gt ) ( 3 )
Từ ( 1 ) ; ( 2 ) ; ( 3 )
\(\Rightarrow\) tam giác \(ABE\) đều
Chứng minh câu d:
Ta có: AE = AB < AC
=> E thuộc canh AC
\(\Delta\)ABE đều mà AD vuông BE tại I => AD là đường trung trực của DE => DB = DE (1)
Dễ chứng minh \(\Delta\)ABD = \(\Delta\)AED
=> ^ABD = ^AED => ^B1 = ^DEC ( góc ngoài )
mà ^B1 là góc ngoài của \(\Delta\)ABC tại B => ^B1 > ^C
=> ^DEC > ^C = ^ECD
Xét trong \(\Delta\)DEC có: ^DEC > ^ECD => DC > DE (2)
Từ (1); (2) => DC > DB
cho tam giác ABC vuông tại A , \(\widehat{B}=60^o\). vẽ AH vuông góc với BC \(\left(H\in BC\right)\)
a, so sánh AB và AC , BH và HC
b, lấy D thuộc tia đối của HA sao cho . Chứng minh : \(\Delta AHC=\Delta DHC\)
c, tính góc BDC
Câu hỏi của nguyen anh ngoc ly - Toán lớp 7 - Học toán với OnlineMath
Cho tam giác ABC vuông tại A (góc B bé hơn góc C) Vẽ AH vuông góc BC (H thuộc BC)
a)So sánh AB và AC
b)So sánh BH và CH
c)So sánh AH và BC
Mn giải nhanh hộ với
Xem chi tiết
Cho \(\Delta ABC\) có góc A=120 độ. Góc B-C=30 độ. Trung trực của cạnh BC cắt AC ở D, cắt tia đối của tia AB ở E
a) Tính các góc của tam giác ABC
b) CMR: Góc EBD= góc ECD= góc ADB = 30 độ
c) So sánh 2 góc: EBD và EDC
a/Ta có góc A+góc B+ góc C=180o(định lí)
Mà góc A=120o
--> góc B+ góc C=180o-120o=60o
Mà góc B-góc C=30o
--> góc C=(60-30)/2=15o
--> góc B=15o+30o=45o
Đúng 0
Bình luận (0)
rat can diem
nho ban nao tich gium minh nhe
minh rat cam on
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho \(\Delta ABC\) vuông tại A có AB= 6cm, BC= 10cm
Tính Ac và so sánh các góc \(\Delta ABC\)Trên tia đối của AB lấy D sao cho AD=AB. Gọi K là trung điểm của BC, đường thẳng DK cắt AC tại M.C/m BC=CD và độ dài AMĐường trung trức d của đoạn AC cẳ đường thẳng DC tại Q. C/m B, M, Q thẳng hànga] Áp dụng định lí Py - ta - go vào tam giác vuông ABC có ;
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\) \(AC^2=BC^2-AB^2\)
\(\Leftrightarrow\) \(AC^2=10^2-6^2\)
\(\Leftrightarrow\) \(AC^2=64\)
\(\Rightarrow\) \(AC=8cm\)
Ta có ; \(AB=6cm\) , \(AC=8cm\) , \(BC=10cm\)
\(\Rightarrow\) \(BC\)lớn hơn \(AC\) lớn hơn \(AB\)
\(\Leftrightarrow\) góc \(A\) lớn hơn góc \(B\) lớn hơn góc \(C\) [ theo quan hệ giữa cạnh và góc đối diện ]