Cho tam giác cân chung cạng đáy BC là ABC, MBC và NBC. Chứng minh: A, M, N thẳng hàng.

Những câu hỏi liên quan
cho 3 tam giác MBC,NBC và ABC có chung đáy BC. Chứng minh A,M,N thẳng hàng
207836450 + 386890976 - 746372342
Cho tam giác ABC cân tại A. M là điểm nằm trong tam giác ABC sao cho: góc MAC=MBA=MBC. Gọi N là trung điểm AC. Chứng minh M, M, N thẳng hàng
cho 2 tam giác cân abc và mbc có chung đáy BC . CMR đường thẳng MA là đường trung trực của BC
cho 2 tam giác cân abc và mbc có chung đáy BC . CMR đường thẳng MA là đường trung trực của BC
Ta có: AB=AC => A thuộc đường trung trực của BC (1)
Mặt khác MB=MC => M thuộc đường trung trực BC (2)
Từ (1) và (2) => MA là đường trung trực của BC
Đúng 0
Bình luận (0)
Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
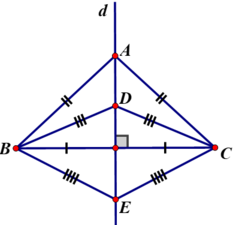
Vì ΔABC cân tại A ⇒ AB = AC
⇒ A thuộc đường trung trực của BC.
Vì ΔDBC cân tại D ⇒ DB = DC
⇒ D thuộc đường trung trực của BC
Vì ΔEBC cân tại E ⇒ EB = EC
⇒ E thuộc đường trung trực của BC
Do đó A, D, E cùng thuộc đường trung trực của BC
Vậy A, D, E thẳng hàng
Đúng 0
Bình luận (0)
Cho ba tam giác cân ABC, DBC, EBC chung đáy BC. Chứng minh rằng ba điểm A, D, E thẳng hàng.
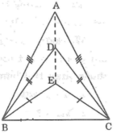
Tam giác ABC cân tại A nên AB = AC
Khi đó A thuộc đường trung trực của BC (1)
Tam giác DBC cân tại D nên DB = DC
Khi đó D thuộc đường trung trực của BC (2)
Tam giác EBC cân tại E nên EB = EC
Khi đó E thuộc đường trung trực của BC (3)
Từ (1), (2) và (3) suy ra: A, D, E thẳng hàng.
Đúng 0
Bình luận (0)
Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh 3 điểm A, D, E thẳng hàng ?
Hướng dẫn:
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
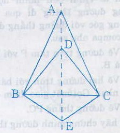
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
Đúng 0
Bình luận (0)
Hướng dẫn:
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC

Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
Đúng 0
Bình luận (0)
cho ba tam giác cân ABC;DBC;EBC có chung đáy BC .Chứng minh ba điểm A;D;E thẳng hàng ?
tam giác ABC ; DBC ; EBC lần lượt cân tại đỉnh A; D; E
=> AB = AC => A thuộc đường trung trưc của đoạn thẳng BC
DB = DC => D thuộc đường trung trực của đoạn thẳng BC
EB = EC => E thuộc đường trung trực của đoạn thẳng BC
Vậy A; D; E đều thuộc đường trung trực của đoạn thẳng BC hay A; D; E thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Vẽ ra ngoài tam giác ABC tam giác cân BCM có đáy BC và góc ở đáy 15o . Vẽ tam giác đều ABN (N thuộc nửa mặt phẳng bờ AB có chứa C). Chứng minh 3 điểm B, M, N thẳng hàng.
Bài làm
Vì tam giác NAB và tam giác đều
=> NA = NB = BA
=> Góc N = góc NBA = góc NAB = 60o
Ta có: Góc ABM = NAB + N ( tính chất goác ngoài tam giác )
hay Góc ABM = 60o + 60o
=> Góc ABM = 120o
Lại có: Góc ABC + CBM = ABM
hay góc ABC + 15o = 120o
=> Góc ABC = 120o - 15o
=> Góc ABC = 105o
Ta có: Góc NBM = ABN + ABC + CBM
hay góc NBM = 60o + 105o + 15o
=> góc NBM = 180o
Do đó góc NBM là góc bẹt
=> 3 điểm B, M, N thẳng hàng ( đpcm )
# Chúc bạn học tốt #
Đúng 0
Bình luận (1)
hình như bạn vẽ sai hình thì phải.
Cho mình hỏi nếu mình vẽ hình sai thì sao mình lại được Online Math chọn làm câu trả lời đúng vậy ạ :)?

















