△ABC có AC=6,CB=4 ,trung tuyến BM=\(\sqrt{14}\) /2 .tính cosA và Sabc

Những câu hỏi liên quan
cho tam giác ABC có AC=4,AC=6 và trung tuyến BM=3 .tính độ dài cạnh BC và trung tuyến AN
Cho tam giác ABC vuông tại A có BC=5a và trung tuyến BM = a\(\sqrt{3}\).Tính AB và AC
Cho tam giác ABC có dướng phân giác AD, đường cao CH và đường trung tuyến BM giao nhau tại I. Vẽ MN song song với AB ( N thuộc HC). Tính tỉ số cosB/cosA theo các cạnh của tam giác ABC
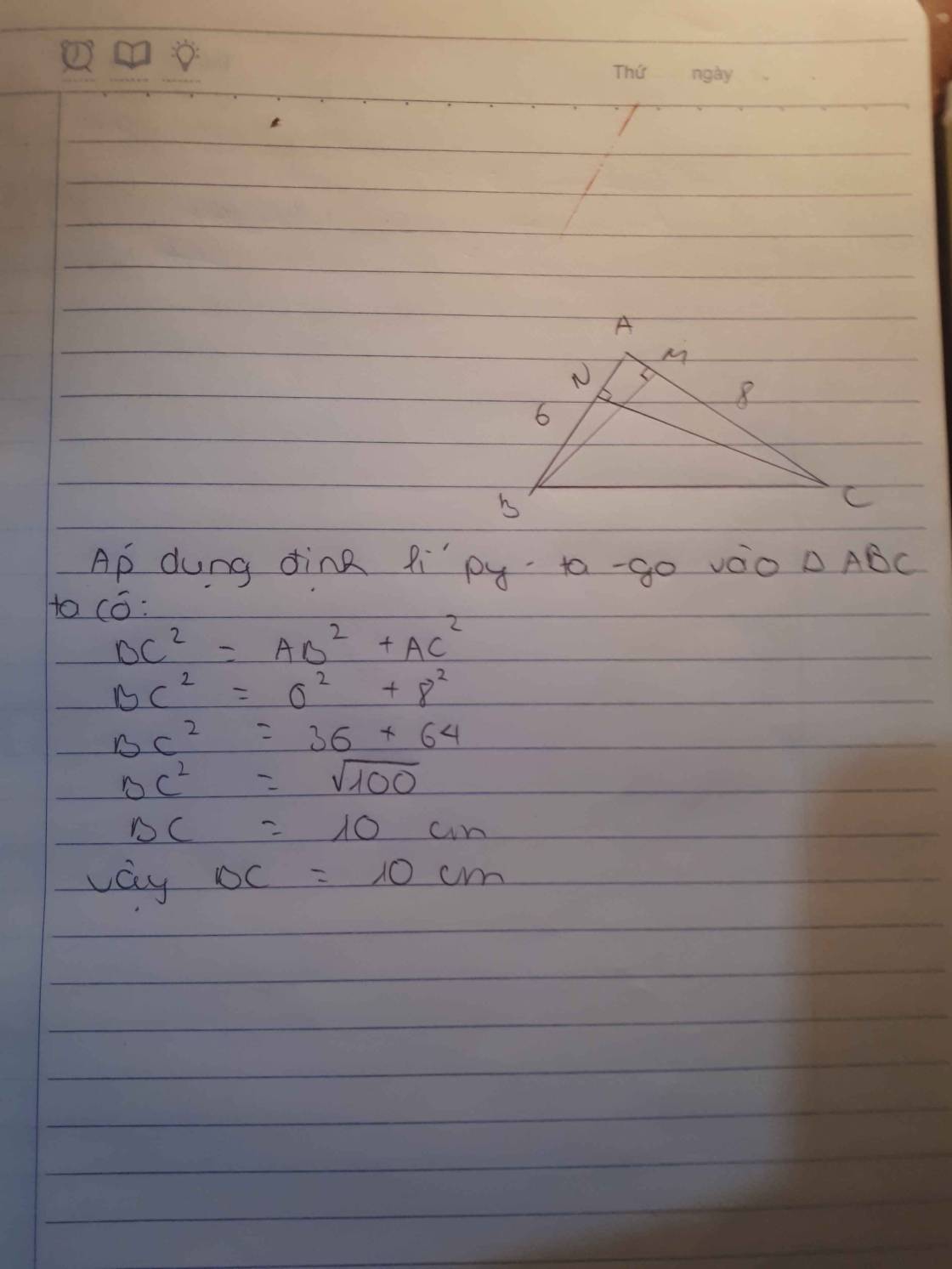
Cho tam giác ABC có AB = 6,AC = 8 và hai đường trung tuyến BM,CN vuông góc với nhau. Tính độ dài cạnh BC
cho ΔABC đường trung tuyến BM. Trên đoạn BM lấy điểm D sao cho BD=\(\dfrac{1}{3}\)BM. Tia AD cắt BC ở K và cắt đường thẳng qua B song song với AC ở E.
a) chứng minh ΔBKE∼ΔMDA.
b) cho BE=3cm. tính AC
c) tính SABC biết SABE=20 cm2.
cho tam giác ABC, phân giác AD và đường cao CH và trung tuyến BM gặp nhau tạ 1 điểm
Chứng minh AB. cosA = BC. cosB
△ABC có trung tuyến AM, lấy trên AM i bất kì, BI cắt AC tại E, biết SAIE =4cm2 ,SCIE=12cm2 tính SABC
\(\dfrac{S_{AIE}}{S_{CIE}}=\dfrac{4}{12}=\dfrac{1}{3}\)
=>AE/CE=1/3
=>AE=1/3CE
Kẻ MK//BE(K thuộc EC)
=>K là trung điểm của CE
=>EK=1/2CE
=>CE=2EK
=>AE=1/3*2*EK=2/3*EK
Xet ΔAMK có IE//MK
nên AI/AM=AE/AK=2/5
=>\(\dfrac{S_{AIC}}{S_{MAC}}=\dfrac{2}{5}\)
=>\(S_{MAC}=40\left(cm^2\right)\)
=>\(S_{ACB}=80\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AD là phân giác, đường cao CH và trung tuyến BM cắt nhau tại I. Vẽ MN // AB (N thuộc HC). Chứng minh:
a) HB/MN = AB/AM
b) AB.AH = AC.HB
c) cosA/cosB = BC/AB
Câu 1:a) Delta ABCcó BD và CE là 2 đường trung tuyến và BD^2+CE^2frac{9}{4}BC^2. C/m BD⊥CEtại G.b)Delta ABCcó BCa, ACb, ABc. Hai đường trung tuyến AM và BN vuông góc với nhau tại G. C/ma^2+b^25c^2Câu 2: Cho Delta ABCcân tại A có BCa và cạnh bên bằng cạnh huyền của tam giác vuông cân có cạnh góc vuông bằng a. Tính độ dài đường trung tuyến BM của Delta ABCtheo a.Câu 3: Cho Delta ABC, trung tuyến CD. Đường thẳng qua D và song song với BC cắt AC tại E. Đường thẳng qua D và song song với AC cắt BC tạ...
Đọc tiếp
Câu 1:
a) \(\Delta ABC\)có BD và CE là 2 đường trung tuyến và \(BD^2+CE^2=\frac{9}{4}BC^2\). C/m \(BD⊥CE\)tại G.
b)\(\Delta ABC\)có BC=a, AC=b, AB=c. Hai đường trung tuyến AM và BN vuông góc với nhau tại G. C/m\(a^2+b^2=5c^2\)
Câu 2: Cho \(\Delta ABC\)cân tại A có BC=a và cạnh bên bằng cạnh huyền của tam giác vuông cân có cạnh góc vuông bằng a. Tính độ dài đường trung tuyến BM của \(\Delta ABC\)theo a.
Câu 3: Cho \(\Delta ABC\), trung tuyến CD. Đường thẳng qua D và song song với BC cắt AC tại E. Đường thẳng qua D và song song với AC cắt BC tại F. Trên tia đối của tia BD lấy N sao cho BN=BD. Trên tia đối của tia CB lấy M sao cho CM=CF, gọi giao điểm của MD và AC là K. C/m N, F, K thẳng hàng.
Câu 4: Cho \(\Delta ABC\)có BC=2AB. Gọi M, I lần lượt là trung điểm của BC và BM. C/m AC=2AI và AM là tia phân giác của\(\widehat{CAI}\).
Câu 5: Cho \(\Delta ABC\),trung tuyến BM. Trên tia BM lấy 2 điểm G và K sao cho \(BG=\frac{2}{3}BM\) và G là trung điểm BK, gọi N là trung điểm KC , GN cắt CN tại O. C/m: \(GO=\frac{1}{3}BC\)
(Bạn giải được câu nào thì giải, nhớ vẽ hình và ghi lời giải đầy đủ)