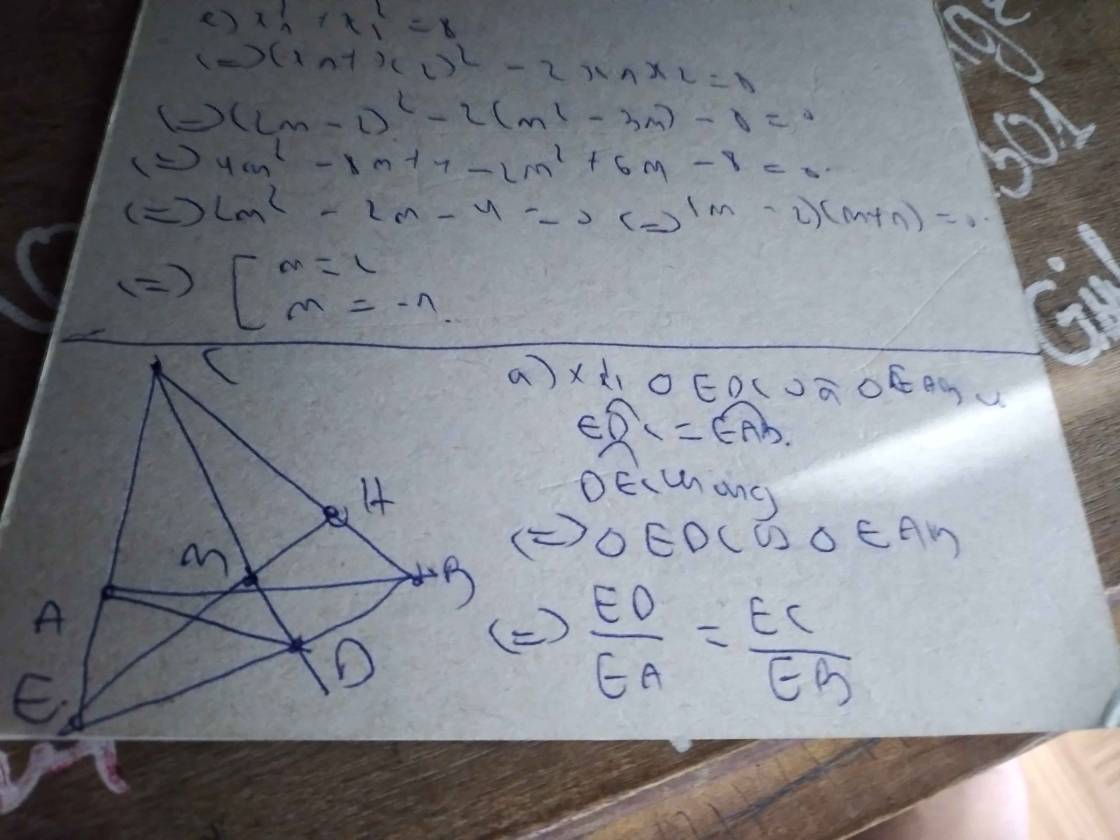
\(Cho tam giác ABC vuông cân tại A. Trên AB lấy M. Kẻ BD vuông góc với CM, BD cắt CA tại E.Chứng minh rằng: a. EB.ED = EA.EC b. BD . BE CA. CE = BC2 c. Góc ADE = 45o\)

Những câu hỏi liên quan
Cho tam giác ABC vuông cân tại A. Trên AB lấy M. Kẻ BD vuông góc với CM, BD cắt CA tại E.Chứng minh rằng:
a. EB.ED = EA.EC
b. BD . BE + CA. CE = BC2
c. Góc ADE = 45o
Cho tam giác ABC vuông cân tại A. Trên AB lấy M. Kẻ BD vuông góc với CM, BD cắt CA tại E.Chứng minh rằng:
a. EB.ED = EA.EC
b. BD . BE + CA. CE = BC2
c. Góc ADE = 45o
d.Gọi K là hình chiếu của M trên bc kẻ ki vuông ab và kh vuông ac tìm vị trí của m để diện tích aikh lớn nhất
Cho tam giác ABC cân tại A. Trên cạch AB lấy M . Kẻ BD vuông góc với CM cắt CA ở E . CM
a)EB.ED=EA.EC
b)AED=45o
c)BD.BE+CA.CE=BC2
Cho tam giác ABC vuông cân , góc A bằng 90 độ. Trên cạnh AB lấy điểm M bất kì , kẻ BD vuông góc với CM , BD cắt AC ở E . Chứng minh rằng
a) chứng minh EB.ED= EA.EC
b) BD.BE+ CA. CE= BC2
c) chứng minh góc ADE bằng 45 độ
bài giảng ở đây nha
Câu hỏi của Quỳnh Hoa Lenka - Toán lớp 8 | Học trực tuyến
vào thống kê hỏi đáp của mình có chữ màu xanh ở câu trả lời này nhấn zô đó sẽ ra
hc tốt ~:B~
Đúng 0
Bình luận (0)
#)Bạn tham khảo nha :
https://h.vn/hoi-dap/question/233221.html
Đúng 0
Bình luận (0)
a) Ta có tam giác ABC vuông cân tại A (đề bài)
=> Góc BAC = EAB = 90o
Vì BD vuông góc với CM (đề bài)
=> Góc BDC = EDC = 90o
Xét tam giác EAB và tam giác EDC có:
+) Góc BEC chung
+) Góc EAB = góc EDC = 90o
=> Tam giác EAB ~ tam giác EDC (g.g)
=> EA/ED = EB/EC (tính chất 2 tam giác đồng dạng)
=> EA.EC = EB.ED (tính chất tỷ lệ thức)
b) Ta có CD vuông góc với BE, AB vuông góc với EC mà CD cắt AB tại M
=> M là trực tâm của tam giác BEC
Kẻ EM vuông góc với BC tại H.
Xét tam giác HBE vuông tại H và tam giác DBC vuông tại D có:
Góc EBC chung
=> Tam giác HBE ~ Tam giác DBC (g.g)
=> HB/BD = BE/BC (tính chất 2 tam giác đồng dạng)
=> HB.BC = BD.BE (1)
Xét tam giác HCE vuông tại H và tam giác ACB vuông tại A có:
Góc ECB chung
=> Tam giác HCE ~ tam giác ACB (G.G)
=> HC/AC = CE/BC
=> HC.BC = AC.CE (2)
Từ (1)(2) => BD.BE + CA.CE = HB.BC + HC.BC = BC (HB + HC) = BC2
c) Ta có EA.EC = EB.ED (cmt) => ED/EC = EA/AB (Tính chất tỷ lệ thức)
Xét tam giác EDA và tam giác ECB có:
+) ED/EC = EA/AB (cmt)
+) Góc BEC chung
=> Tam giác EDA ~ tam giác ECB (g.g)
=> Góc ADE = góc BCE = 45O (Tính chất 2 tam giác đồng dạng)
Cho tam giác ABC vuông cân tại A. Trên AB lấy M. Kẻ BD vuông góc với CM, BD cắt CA tại E.Chứng minh rằng:
a. EB.ED = EA.EC
b. BD . BE + CA. CE = BC2
c. Góc ADE = 45o
a)
Tam giác AEB vuông tại A và tam giác DEC vuông tại D có:
AEB = DEC
=> Tam giác AEB ~ Tam giác DEC (g - g)
=> \(\dfrac{AE}{DE}=\dfrac{EB}{EC}\)
=> EB . DE = AE . EC
b)
Tam giác EBC có: CD là đường cao và BA là đường cao
CD cắt BA tại M
=> M là trực tâm của tam giác EBC
=> EM _I_ tại H (H thuộc BC)
Tam giác HBE vuông tại H và tam giác DBC vuông tại D có:
HBE = DBC
=> Tam giác HBE ~ Tam giác DBC (g - g)
=> \(\dfrac{HB}{DB}=\dfrac{BE}{BC}\)
=> DB . BE = HB . BC
Tam giác HCE vuông tại H và tam giác ACB vuông tại A có:
HCE = ACB
=> Tam giác HCE ~ Tam giác ACB (g - g)
=> \(\dfrac{HC}{AC}=\dfrac{CE}{CB}\)
=> HC . CB = AC . CE
Ta có : DB . BE + AC . CE = HB . BC + HC . CB = BC . (HC + HB) = BC . BC = BC2
c)
Tam giác EDA và tam giác ECB có:
DEA = CEB
\(\dfrac{DE}{CE}=\dfrac{EA}{EB}\) (EB . DE = AE . EC)
=> Tam giác EDA ~ Tam giác ECB (c - g - c)
=> ADE = BCE = 450 (tam giác ABC vuông cân tại A)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông cân : Â=90độ , Trên canh AB lấy điểm M, kẻ BD cắt CA ở E. Chứng minh
a,EB.ED=EA.EC
b,BD.BE+CA.CE=BC.BC
c,góc ADE=45độ
BK
Toán lớp 6Hình học
Trần Ngọc Bảo An 31/07/2015 lúc 21:18
a) Vì M, B thuộc 2 tia đối nhau CB và CM
=> C nằm giữa B và M
=> BM = BC + CM =8 (cm)
b) Vì C nằm giữa B, M
=> Tia AC nằm giữa tia AB và tia AM
=> góc CAM = góc BAM - góc BAC = 20 độ
c) Ta có :
Góc xAy = góc xAC + góc CAy = 1/2 góc BAC + 1/2 góc CAM
= 1/2 (góc BAC + góc CAM) = 1/2 góc BAM 1/2 x 80 độ = 40 độ
d) Nếu K thuộc CM => C nằm giữa B và K
=> BK = BC + CK 6 (cm)
Nếu K thuộc CB => K nằm giữa C và B
=> BK = BC = CK = 4 (cm)
Đúng 5 Phạm Thị Thúy Hằng đã chọn câu trả lời này.
Kunzy Nguyễn 31/07/2015 lúc 21:06
a) MB = 5,5 + 3 = 8,5 cm
b) CAM = 20 độ
c) TH1: K nằm trên đoạn BC => BK = 5,5 - 1 = 4,5 cm
TH2: K nằm trên đoạn CM => BK = 5,5 + 1 = 6,5 cm
Đúng 1
Đúng 0
Bình luận (0)
cho tam giác ABC vuông cân tại A . trên cạnh AB lấy điểm M kể BD vuông góc CM . BD cắt CA tại e . CMR a , BE.ED = AE.EC b, BD.BE =+ AC .EC = BC^2 C. GÓC ADE = 45 ĐỘ
BÀI 1 cho tam giác ABC vuông tại A.Kẻ BD là phân giác của góc B.Kẻ AI vuông góc BD tại I.AI cắt BC tại Ea) chứng minh ABEBb) chứng minh tam giác BED vuôngc) DE cắt AB tại F, chứng minh AE//FCBÀI 2 cho tam giác ABC cân tại A, có BD và CE là hai đường trung tuyến cắt nhau tại Ia) chứng minh tam giác IBC cânb)lấy O thuộc tia IC sao cho IOIE.Gọi K là trung điểm của IA.Chứng minh AO, BD, CK đồng quyBÀI 3 cho tam giác ABC cân tại A, kẻ tia phân giác của góc BAC cắt BC tại H.Biết AB15cm, BC18cma)so sán...
Đọc tiếp
BÀI 1 cho tam giác ABC vuông tại A.Kẻ BD là phân giác của góc B.Kẻ AI vuông góc BD tại I.AI cắt BC tại E
a) chứng minh AB=EB
b) chứng minh tam giác BED vuông
c) DE cắt AB tại F, chứng minh AE//FC
BÀI 2 cho tam giác ABC cân tại A, có BD và CE là hai đường trung tuyến cắt nhau tại I
a) chứng minh tam giác IBC cân
b)lấy O thuộc tia IC sao cho IO=IE.Gọi K là trung điểm của IA.Chứng minh AO, BD, CK đồng quy
BÀI 3 cho tam giác ABC cân tại A, kẻ tia phân giác của góc BAC cắt BC tại H.Biết AB=15cm, BC=18cm
a)so sánh góc A và góc C
b)chứng minh rằng tam giác ABH = tam giác ACH
c)vẽ trung tuyến BD của tam giác ABC cắt AH tại G.Chứng minh rằng: tam giác AEG = tam giác ADG
d)tính độ dài AG
e) kẻ đường thẳng CG cắt AB ở E, chứng minh rằng: tam giác AEG = tam giác ADG
BÀI 4 cho tam giác ABC vuông tại A, trên BC lấy điểm D sao cho BA=BD.Qua D kẻ đường vuông góc với BC cắt AC tại E, qua C kẻ đường vuông góc với BE tại H cắt AB tại F
a)chứng minh tam giác ABE = tam giác DBE
b) chứng minh tam giác BCF cân
c) chứng minh 3 điểm F.D,E thẳng hàng
d)trên cạnh CB lấy điểm M sao cho CA=CM.Tính số đo góc DAM
BÀI 5 cho tam giác ABC cân tại A, kẻ BD vuông góc AC, kẻ CE vuông góc AB, BD và CE cắt nhau tại I
a)chứng minh rằng tam giác BDC = tam giác CEB
b)so sánh góc IBE và góc ICD
c) đường thẳng AI cắt BC tại H, chứng minh AI vuông góc BC tại H
BÀI 6 cho tam giác ABC vuông tại A, biết AB=6cm, AC=8cm
a)tính BC
b)trung trực của BC cắt AC tại D và cắt AB tại F, chứng minh góc DBC=DCB
c) trên tia đối của tia DB lấy E sao cho DE=DC, chứng minh tam giác BCE vuông và DF là phân giác góc ADE
d) chứng minh BE vuông góc FC
BÀI 1 cho tam giác ABC vuông tại A.Kẻ BD là phân giác của góc B.Kẻ AI vuông góc BD tại I.AI cắt BC tại E
a) chứng minh AB=EB
b) chứng minh tam giác BED vuông
c) DE cắt AB tại F, chứng minh AE//FC
BÀI 2 cho tam giác ABC cân tại A, có BD và CE là hai đường trung tuyến cắt nhau tại I
a) chứng minh tam giác IBC cân
b)lấy O thuộc tia IC sao cho IO=IE.Gọi K là trung điểm của IA.Chứng minh AO, BD, CK đồng quy
BÀI 3 cho tam giác ABC cân tại A, kẻ tia phân giác của góc BAC cắt BC tại H.Biết AB=15cm, BC=18cm
a)so sánh góc A và góc C
b)chứng minh rằng tam giác ABH = tam giác ACH
c)vẽ trung tuyến BD của tam giác ABC cắt AH tại G.Chứng minh rằng: tam giác AEG = tam giác ADG
d)tính độ dài AG
e) kẻ đường thẳng CG cắt AB ở E, chứng minh rằng: tam giác AEG = tam giác ADG
BÀI 4 cho tam giác ABC vuông tại A, trên BC lấy điểm D sao cho BA=BD.Qua D kẻ đường vuông góc với BC cắt AC tại E, qua C kẻ đường vuông góc với BE tại H cắt AB tại F
a)chứng minh tam giác ABE = tam giác DBE
b) chứng minh tam giác BCF cân
c) chứng minh 3 điểm F.D,E thẳng hàng
d)trên cạnh CB lấy điểm M sao cho CA=CM.Tính số đo góc DAM
BÀI 5 cho tam giác ABC cân tại A, kẻ BD vuông góc AC, kẻ CE vuông góc AB, BD và CE cắt nhau tại I
a)chứng minh rằng tam giác BDC = tam giác CEB
b)so sánh góc IBE và góc ICD
c) đường thẳng AI cắt BC tại H, chứng minh AI vuông góc BC tại H
BÀI 6 cho tam giác ABC vuông tại A, biết AB=6cm, AC=8cm
a)tính BC
b)trung trực của BC cắt AC tại D và cắt AB tại F, chứng minh góc DBC=DCB
c) trên tia đối của tia DB lấy E sao cho DE=DC, chứng minh tam giác BCE vuông và DF là phân giác góc ADE
d) chứng minh BE vuông góc FC
Đúng 1
Bình luận (0)
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm D, kẻ CE vuông góc với BD, CE cắt AB tại K. Chứng minh rằng:
a) Bốn điểm A, B, C, E cùng thuộc một đường tròn.
b) BC^2CDcdot CA+BDcdot BE
Đọc tiếp
Cho tam giác \(ABC\) vuông tại \(A\). Trên cạnh \(AC\) lấy điểm \(D\), kẻ \(CE\) vuông góc với \(BD\), \(CE\) cắt \(AB\) tại \(K\). Chứng minh rằng:
\(a\)) Bốn điểm \(A,\) \(B,\) \(C,\) \(E\) cùng thuộc một đường tròn.
\(b\)) \(BC^2=CD\cdot CA+BD\cdot BE\)
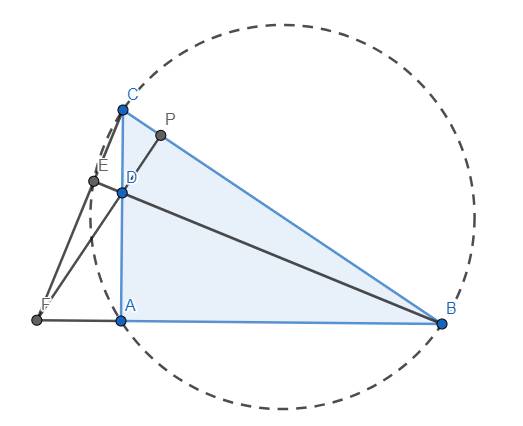
a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.
b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)
CMTT, ta có \(BD.BE=BC.BP\)
Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.
Đúng 4
Bình luận (0)