Cho tam giác ABC có , C = 45o, BC = a. Hãy tính AB, AC và diện tích
tam giác ABC.

Những câu hỏi liên quan
cho tam giác ABC vuong tại A có AB =5cm AC=12 dường cao AH
1)tính BC ,AH
2)gọi D và E lần lượt là hình chiếu của H trên AB và AC. cmr : diện tíchtam giác ADE=sin2 B.sin2C.dien tích tam giac ABC
1,
+, tính BC
\(BC^2=AB^2+AC^2\Rightarrow BC^2=5^2+12^2=25+144=169\)
\(\Rightarrow BC=\sqrt{169}=13\left(cm\right)\)
+, Tính AH
\(AH\cdot BC=AB\cdot AC\Rightarrow AH=\frac{AB\cdot AC}{BC}=\frac{5\cdot12}{13}=\frac{60}{12}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC và tam giác DEF có: ABDE, BCEF, ACDFNếu
A
^
45
o
, thì số đo
D
^
là A. 45
°
B. 54
°
C. 30
°
D. 50
°
Đọc tiếp
Cho tam giác ABC và tam giác DEF có: AB=DE, BC=EF, AC=DF
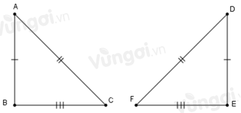
Nếu A ^ = 45 o , thì số đo D ^ là
A. 45 °
B. 54 °
C. 30 °
D. 50 °
Cho tam giác ABC,D là điểm nằm bên cạnh BC. Tính diện tíchtam giácADC,biết diện tích tam giác ABD=48 cm vuông và BD =16cm;DC=6cm
Chiều cao của hình tam giác ABC là :
48 * 2 : 16 = 6 (cm)
Diện tích hình tam giác ADC là :
6 * 6 :2 = 18 (cm2)
Đ/S : 18 cm2
Đúng 0
Bình luận (0)
Chiều cao của tam giác ABC là :
48 x 2 : 16 = 6 ( cm )
Diện tích của tam giác ADC là :
6 x 6 : 2 = 18 ( cm2 )
Đúng 0
Bình luận (0)
Cho tam giác ABC ( vuông ở A ) . Có AB = 30 cm, AC = 40 cm ,BC = 50 cm . D và E trên AB và AC . Cho biết diện tích hình thang BDEC có chiều cao là 6 cm
a, Hãy tính 3 đường cao tam giác ABC
b,Tính diện tích tam giác ADE
Bài 2. 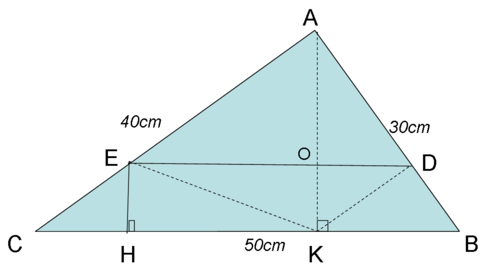
a) Trong tam giác vuông thì 2 cạnh góc vuông cũng chính là 2 đường cao của tam giác đó.
Vậy đường cao AB = 30 cm ; đường cao AC = 40 cm
Đường cao tam giác ABC còn lại đỉnh A là : 30 x 40 : 50 = 24 (cm)
b) S_ECK + S_DKB = CK x 6 : 2 + KB x 6 : 2 = (CK+KB) x 6 : 2 = 50 x 3 = 150 (cm2)
S_AEKD = 30 x 40 : 2 - 150 = 450 (cm2)
Xét tam giác AED và EDK chung đáy ED chiều cao AO = 24 - 6 = 18 (cm)
Tỉ lệ AO/OK = 18/6 = 3. Vậy S_AED = 3 x S_EDK
Diện tích tam giác AED là : 450 : (1+3) x 3 = 337,5 (cm2)
Đúng 0
Bình luận (0)
WTF!!!!!!!!!! Khó Zậy!!!
cho ABC vuông tại A có BC dài 20cm, góc C bằng 40°. Đường cao AH hãy Tính AB,AC,AH,BH và diện tích tam giác ABC
Cho tam giác ABC, có BC 6 cm,
B
^
60
0
và
C
^
40
0
. Hãy tính:a, Chiều cao CH và cạnh ACb, Diện tích tam giác ABC
Đọc tiếp
Cho tam giác ABC, có BC = 6 cm, B ^ = 60 0 và C ^ = 40 0 . Hãy tính:
a, Chiều cao CH và cạnh AC
b, Diện tích tam giác ABC
a, Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông HCB chúng ta có
CH = 3 3 cm; A C sin C ≈ 5 , 28 c m
b, Tương tự, cũng áp dụng Pytago hoặc hệ thức giữa cạnh và góc trong tam giác vuông, tính được:
AH, BH => AB = 3,93cm. Ta có: S = 1 2 . 3 3 . 3 , 93 ≈ 10,21 c m 2
Đúng 0
Bình luận (0)
1 ) Cho tam giác ABC có góc A nhọn , AB=4 , AC=5 và diện tích tam giác ABC =8 . Tính BC
2 ) Cho tam giác ABC có AB=3 , góc ACB = 45° , góc ABC = 60° . Tính BC
em mới học lớp 7 hà
năm nay lên lớp 8 =)))))
Đúng 0
Bình luận (0)
1)Ta có: \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
\(\Leftrightarrow8=\dfrac{1}{2}\times4\times5\times sinA\)
\(\Leftrightarrow\sin A=0,8\)
Lại có: \(\left(\sin A\right)^2+\left(\cos A\right)^2=1\Leftrightarrow\cos A=0,6.\)
Áp dụng định lí hàm số cosin:
\(BC^2=AB^2+AC^2-2AB\times AC\times\cos A\)
\(\Leftrightarrow BC^2=4^2+5^2-2\times4\times5\times0,6=17\)
\(\Leftrightarrow BC=\sqrt{17}.\)
2) Trong \(\Delta ABC\) có: \(g\text{ó}cA+g\text{óc}B+g\text{óc}C=180^o\)
=> BAC=75o.
Áp dụng định lí hàm số sin:
\(\dfrac{AB}{\sin C}=\dfrac{BC}{\sin A}\Leftrightarrow\dfrac{3}{\sin45^o}=\dfrac{BC}{\sin75^o}\)
\(\Leftrightarrow BC=\dfrac{3+3\sqrt{3}}{2}\).
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6 cm ; AC = 4,5 cm ; BC = 7,5 cm a) chứng minh tam giác ABC vuông tại A b) Kẻ đường cao AH (H thuộc BC) tính BH, HC, AH và góc B,C của tam giác c) Tính diện tích tam giác ABC d) tìm vị trí điểm M để diện tích tam giác ABC bằng diện tích tam giác MBC
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC, hai đường trung tuyến BM và CN cắt nhau tại G. Biết BC =10cm, BM =12cm, CN =9cm.Tính diện tíchtam giác ABC và diện tích tứ giác BNMC





















