Viết nghiệm tổng quát của hệ phương trình : 3x + y = 5
Những câu hỏi liên quan
Cho pt 3x - y = 5 a) Hãy viết nghiệm tổng quát rồi tìm một nghiệm nguyên dương của phương trình b) Biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ Oxy
Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.
a) Tìm nghiệm tổng quát của mỗi phương trình trên.
b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong cùng một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.
a) + Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔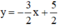 
Vậy phương trình (2) có nghiệm tổng quát là :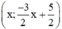 
(x ∈ R).
b) Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) :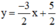 
Chọn x = 0 ⇒ y = 2,5.
Chọn y = 0 ⇒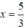 
⇒ (d’) đi qua hai điểm (0; 2,5) và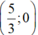 
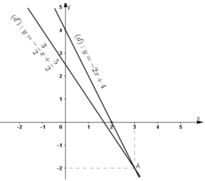
Hai đường thẳng cắt nhau tại A(3; -2).
Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2).
Đúng 1
Bình luận (0)
GIÚP EM VỚI Ạ,EM CẦN GẤP Ạ
1)Cho phương trình 3x+2y=7.
Tìm nghiệm tổng quát của phương trình,tìm nghiệm nguyên của phương trình
2)Cho hệ phương trình: mx+y=1
4x+5y=3
Giải hệ phương trình với m= -2 bằng 2 cách (phương pháp thế,phương pháp cộng đại số)
Bài 1:
3x+2y=7
\(\Leftrightarrow3x=7-2y\)
\(\Leftrightarrow x=\dfrac{7-2y}{3}\)
Vậy: \(\left\{{}\begin{matrix}y\in R\\x=\dfrac{7-2y}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.
a) Tìm nghiệm tổng quát của mỗi phương trình trên.
b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong mỗi một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.
a) . Do đó phương trình có nghiệm dạng tổng quát như sau:
hoặc
b) Vẽ (d1): 2x + y = 4
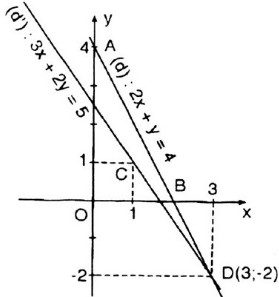
- Cho x = 0 => y = 4 được A(0; 4).
- Cho y = 0 => x = 2 được B(2; 0).
Vẽ (d2): 3x + 2y = 5
- Cho x = 0 => y = 
được C(0; ).
- Cho y = 0 => x = 
được D(; 0).
Hai đường thẳng cắt nhau tại M(3; -2).
Thay x = 3, y = -2 vào từng phương trình ta được:
2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)
Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.
Đúng 0
Bình luận (0)
Cho hai phương trình 2x + y = 4 và 3x + 2y = 5.
Tìm nghiệm tổng quát của mỗi phương trình trên
+ Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔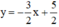 
Vậy phương trình (2) có nghiệm tổng quát là :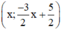 
(x ∈ R).
Đúng 0
Bình luận (0)
Cho phương trình : 3x - y 9. Nghiệm tổng quát của phương trình là: A.
x
∈
R
y
3
x
+
9
B.
x
∈
R...
Đọc tiếp
Cho phương trình : 3x - y = 9. Nghiệm tổng quát của phương trình là:
A. x ∈ R y = 3 x + 9
B. x ∈ R y = 3 x - 9
C. x ∈ R y = x 3 - 1
D. x ∈ R y = x 3 + 1
Đáp án B
Ta có: Do đó, nghiệm tổng quát của phương trình đã cho là
x ∈ R y = 3 x - 9
Đúng 0
Bình luận (0)
Cho phương trình: x + 2y = 5. Hãy viết công thức tính nghiệm tổng quát của phương trình Và tìm m để phương trình có cặp nghiệm (x ; y) = (m2 ; -2)
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó: 3x – y = 2
3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
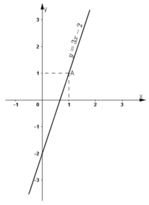
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x =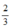 
thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (
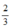; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (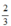
; 0) và (0; -2).
Đúng 0
Bình luận (0)
Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau: 3x – 2y = 6
3x - 2y = 6
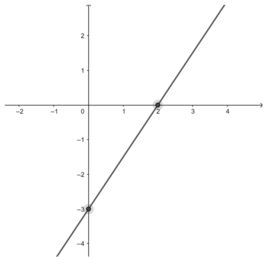
Chọn x = 0 ⇒ y = -3. Đường thẳng đi qua điểm (0; -3)
Chọn y = 0 ⇒ x = 2. Đường thẳng đi qua điểm (2; 0)
Vậy đường thẳng 3x - 2y = 6 đi qua hai điểm (0; -3) và (2; 0)
Đúng 0
Bình luận (0)
Cho phương trình 3x + y = 2
a) viết công thức nghiệm tổng quát của phương trình trên ?
b) Chứng minh đường thẳng y = (m^2 - 1 )x + m^2 - 5 , m khác 1 và -1 luôn đi qua một điểm cố định