Đường tròn tâm O có bán kính OB, góc AOB =60o. Cho π≃3,14. Tính số đo cung lớn và cung nhỏ AmB

Những câu hỏi liên quan
Cho tam giác cân AOB có góc AOB bằng 110 độ.Vẽ đường tròn tâm O , bán kính OA. Gọi C là một điểm trên đường tròn O , biết số đo cung AC=40 độ.Tính số đo cung nhỏ BC và cung lớn BC.
góc COB=40+110=150 độ
=>sđ cung nhỏ BC=150 độ
sđ cung lớn BC=360-150=210 độ
Đúng 0
Bình luận (0)
Cho tam giác cân AOB có góc AOB bằng 110 độ.Vẽ đường tròn tâm O , bán kính OA. Gọi C là một điểm trên đường tròn O , biết số đo cung AC=40 độ.Tính số đo cung nhỏ BC và cung lớn BC.
Cho em xin lời giải cụ thể với ạ,em cảm ơn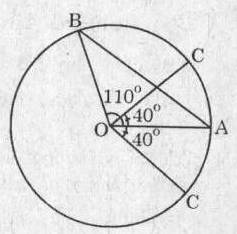
Theo giả thiết: Vì số đo cung \(\stackrel\frown{AC}=40^o\)
\(\Rightarrow\) Góc ở tâm \(\widehat{AOC}=40^o\)
Trường hợp 1: C thuộc cung nhỏ \(\stackrel\frown{AB}\)
- Số đo góc ở tâm \(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}=110^o-40^o=70^o\)
Do vậy:
- Số đo cung nhỏ \(\stackrel\frown{BC}=70^o\)
- Số đo cung lớn \(\stackrel\frown{BC}=360^o-70^o=290^o\)
Trường hợp 2: C thuộc cung lớn \(\stackrel\frown{BC}\)
- Số đo góc ở tâm \(\widehat{BOC}=\widehat{BOA}+\widehat{AOC}=110^o+40^o=150^o\)
Do vậy:
- Số đo cung nhỏ \(\stackrel\frown{BC}=150^o\)
- Số đo cung lớn \(\stackrel\frown{BC}=360^o-150^o=210^o\)
Đúng 0
Bình luận (0)
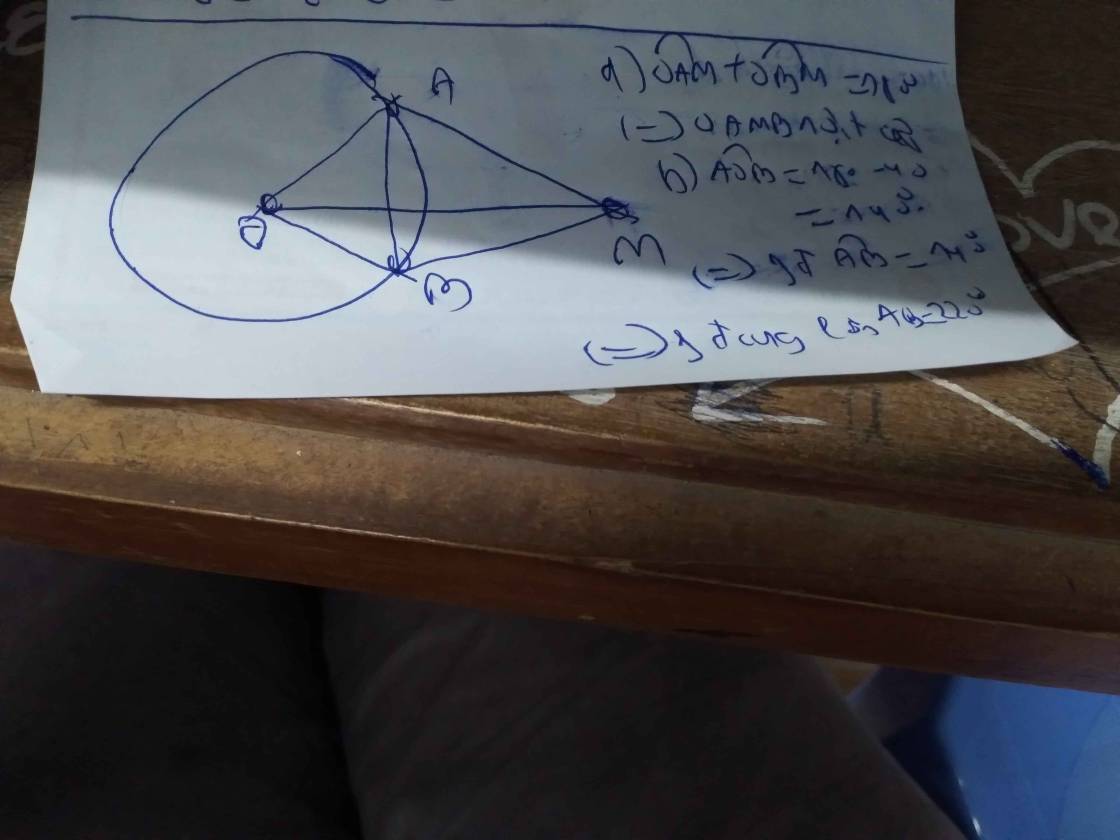
Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết \(\widehat{AMB}=35^o.\)
a) Tính số đo của góc ở tâm tạo bở hai bán kính OA, OB.
b) Tính số đo mỗi cung AB (cung lớn và cung nhỏ).
a) Trong tứ giác AOBM có 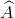 =
= 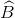 =
= 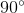 .
.
Suy ra cung AMB +  =
= 
=> cung AMB=  -
- 
=  -
- 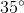
= 
b) Từ 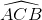 =
=  . Suy ra số đo cung nhỏ AB =
. Suy ra số đo cung nhỏ AB =  và số đo cung lớn AB :
và số đo cung lớn AB :
Cung AB = 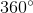 -
-  =
= 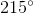
Đúng 0
Bình luận (0)
cho đường tròn tâm (O) bán kính 3cm trên (O) lấy điểm A,B sao cho góc AOB=60 độ. Tính số đo cung nhỏ AB,diện tích hình quạt tròn OAB,độ dài cung lớn AB
* Số đo cung nhỏ AB=góc AOB( góc ở tâm)\(\Rightarrow\) Số đo cung nhỏ AB=60 độ
* Diện ích hình quạt tròn OAB là
\(S=\frac{\pi\times R2\times n}{360}=\frac{\pi\times9\times60}{360}=\frac{3}{2}\pi\approx\frac{3}{2}\times3,14\approx4,71\)cm2
* Số đo cung lớn AB= 360 độ - 60 độ =300 độ
Độ dài cung lớn AB là:
l=3,14*3*300/180=15,7 cm
Đúng 0
Bình luận (0)
Cho đường tròn tâm o bán kính r vẽ dây AB sao cho số đo cung nhỏ AB bằng 1/2 số đo cung lớn AB tính diện tích AOB
Xem chi tiết
Từ O kẻ đg thg vg góc vs AB tại H
=> AH=BH=AB/2 = R căn 3 /2
Theo hệ thức lượng trong tam giác AHO vuông ở H ta có
SIN góc AOH = R căn 3 /2 : R
= căn 3/2 = 60
=> Góc AOB = 2 góc AOH= 2*60 =120
SĐ AB nhỏ =120
SĐ AB lớn = 360 - sđ AB nhỏ = 360 -120 = 240
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, bán kính R=3 cm và hai điểm A,B nằm trên đường tròn (O) sao cho số đo cung lớn bằng 240°. Tính diện tích hình quạt tròn giới hạn bởi hai bán kính OA, OB vsf cung nhỏ AB.
Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm AOB = 60o và bán kính đường tròn là 5,1cm (h.64).
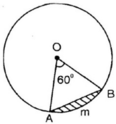
Hình 64
Tam giác OAB là tam giác đều có cạnh R= 5,1 cm.
Công thức tính diện tích tam giác đều cạnh a là: 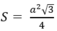
Do đó, diện tích tam giác đều OAB cạnh OA= R = 5,1 cm là: 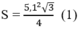
Diện tích hình quạt tròn AOB là:
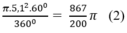
Từ (1) và (2) suy ra diện tích hình viên phân là:
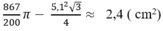
Đúng 0
Bình luận (0)
Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm A O B = 60 o và bán kính đường tròn là 5,1cm (h.64).
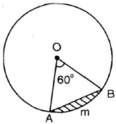
Hình 64
Tam giác OAB là tam giác đều có cạnh R= 5,1 cm.
Công thức tính diện tích tam giác đều cạnh a là: 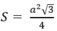
Do đó, diện tích tam giác đều OAB cạnh OA= R = 5,1 cm là: 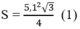
Diện tích hình quạt tròn AOB là:
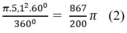
Từ (1) và (2) suy ra diện tích hình viên phân là:
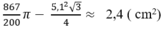
Kiến thức áp dụng
+ Diện tích tam giác đều cạnh a là:
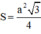
+ Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
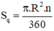
Đúng 0
Bình luận (0)
Cho đường tròn (O; R). Gọi H là trung điểm của bán kính OB. Dây CD vuông góc với OB tại H. Tính số đo cung nhỏ và cung lớn C D ⏜
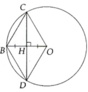
Chứng minh được ∆BOC và ∆BOD là tam giác đều nên suy ra được sđ cung nhỏ C D ⏜ = 120 0 và sđ cung lớn C D ⏜ = 240 0
Đúng 0
Bình luận (0)
cho đường (o) và điểm M bên ngoài đường tròn.Từ M kẻ hai tiếp tuyến MA,MB với đường tròn (A,B là tiếp điểm) a) chứng minh tứ giác MAOB nội tiếp b) Biết góc AMB = 40 độ .Tính số đo góc ở tâm góc AOB và số đo cung nhỏ AB? Số đo cung lớn AB