cho hình vẽ
a) chứng minh aa'//bb''
b) kẻ OH vuông góc aa' tại H. Chứng minh: OH vuông góc bb'
cho hình vẽ
a) chứng minh aa'//bb''
b) kẻ OH vuông góc aa' tại H. Chứng minh: OH vuông góc bb'
giúp mình với
Cho hai đường thẳng aa', bb' song song với nhau. Đường thẳng AB cắt aa', bb' lần lượt tại A, B. Tia phân giác của góc a'AB cắt bb' tại C.
a) Chứng minh : góc ABC = 2.góc ACB;
b) Tia phân giác của góc ABb' cắt aa' tại D. Chứng minh AC và BD vuông góc với nhau.
cho hình bình hành ABCD, qua C vẽ đường thẳng d chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' lần lượt là các đường vuông góc kẻ từ A,B,D đến d. chứng minh rằng AA' = BB'+DD'
Gọi O la giao điểm hai đường chéo hình bình hành
Từ O kẻ OO' vông góc với d tại O'
Ta có O' là trg điểm của A'O (do cùng vuông góc và song song với D' trên duog thẳng d )
suy ra OO'là dg trg bình cua tam giac AAC
suy ra AA' = 2 OO'(1)
Ta có DD' song song BB' ( do cùng vuông óc với d)
suy ra DD' ,BB' là hình thang
Ta có
OO' song song DD' song song BB' (cùng vuông góc d)(a)
Và O là trug điểm DB(b(
Từ (a) và(b) suy ra O là trung điểm D'B'
suy ra OO là dg2 trung bình của bình thang DD' BB'
suy ra OO' là dg trug bình của hình thang DD' BB'
suy ra D'B' =2OO' (2)
Từ (1) và (2) suy ra AA' =BB' +DD'
nhớ cho mình nha
bạn ơi đề bài sai rồi đánh lẽ phải là DD'=AA'+BB' chứ
cho hình bình hành ABCD. Kẻ đường thẳng a tiếp xúc với điểm D. Qua A, B, C hạ các đường thẳng AA', BB', CC' vuông góc vs đường thẳng a. Chứng minh: BB'=AA'+CC'
bn vô các câu hỏi tương tự có đầy đó bn
Cho hình hình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng minh rằng AA' = BB' + DD'
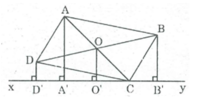
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ∆ ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ∆ ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'
Biết HK vuông góc với bb' tại K
HK vuông góc với aa' tại H, cc' cắt aa' tại M, góc M1=\(45^o\), cc' cắt bb' tại N
a) Chứng minh aa' song song với bb'
b) Tính góc N1
c) Tia phân giác của góc HMN và tia phân giác của góc MNK cắt nhau tại I. Chứng minh MI vuông góc với IN
d) Chứng minh đường thẳng HK cắt đường thẳng cc'
đ) Gọi giao điểm của HK và cc' là E. Chứng minh tam giác KNE có 2 góc bằng nhau
Cho hai đường thẳng aa' ,bb' song song với nhau .đường thẳng AB cắt aa' ,bb' lần lượt tại A,B.Tia phân giác của a'AB cắt bb' tại C
a)chứng minh góc ABC = 2 ACB
b)tia phân giác của góc ABC cắt AC tại D Chứng minh AC và BD vuông góc với nhau
Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điem chung C vs hình bình hành. Gọi AA', BB', DD' là các đuong vuông góc kẻ từ A, B, D đên đuong thẳng xy. Chứng minh AA' = BB' + DD'.
Ai đúng mk tk!!!!^_^
Tìm mãi mới thấy bạn ơi.
Bài làm
Gọi giao điểm 2 đường chéo hình bình hành là O
Ôi mẹ ơi, khó quá, k lm đc, bạn vào câu hỏi tương tự để tham khảo ý
Cho hình lập phương ABCD.A'B'C'D' như hình vẽ.
a) Nêu vị trí tương đối của các cặp đường thẳng BC' và A'D'; DD' và AB; AA’ và A’C'.
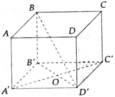
b) Chứng minh A'C' vuông góc với (BB'D'). Từ đó chứng minh A'C' vuông góc BD'.
c) Chứng minh B O = B B ' + 1 4 B ' A ' 2 + B ' C ' 2