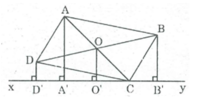
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ∆ ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ∆ ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'











