cho đường tròn tâm O đường kính AB. Qua trung điểm E của OB, kẻ một dường thẳng vuông góc OB, cắt đường tròn O ở M và N. Kẻ dây MP song song AB. Gọi I là điểm chính giữa của cung nhỏ PM. K là giao điểm của OI và PM. CM: KE song song PN

Những câu hỏi liên quan
Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:
a) stackrelfrown{AP}stackrelfrown{BN}.
b) Tứ giác $OKME$ là hình chữ nhật.
c) Ba điểm $P,$ $O,$ $N$ thẳng hàng và $KE // PN$.
Đọc tiếp
Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:
a) \(\stackrel\frown{AP}=\stackrel\frown{BN}\).
b) Tứ giác $OKME$ là hình chữ nhật.
c) Ba điểm $P,$ $O,$ $N$ thẳng hàng và $KE // PN$.
Thọ tested! h heeeee
\(\sqrt{2222}\)
\(\dfrac{1}{22}\)
Giải :
a) Xét (O) có PM // AB
⇒ 2 cung AP và BM bị chắn bởi 2 dây trên sẽ bằng nhau.
mà BM = BN ( △ BMN cân tại B vì có BE vừa là đ/c, đường trung tuyến △)
⇒ cung BM = cung BN
⇒ cung AP = cung BN
b) Xét (O) có OI đi qua điểm chính giữa của PM (gt)
⇒ OI vuông góc với dây PM tại K
⇒góc OKM = 90 độ.
Xét tứ giác OKME có 3 góc vuông : góc OKM = 90 độ (cmt),
góc MEO = 90 độ ( MN vuông góc với OB tại E
góc EMK = 90 độ ( vì PM//AB, AB vuông góc với MN ⇒ PM vuông góc với MN tại M )
⇒ OKME là hcn
c) Ta có : góc OPI = góc NOE ( vì 2 góc đông vị, MP//AB)
mà góc OPI + góc POI = 90 độ ( △POK vuông tại K )
⇒góc NOE + góc POI = 90 độ
⇒ góc NOE + góc POI + góc IOE = 90 + 90 = 180 độ
⇒ P,O,N thẳng hàng
- Xét △ PMN có KE đường TB ( K trđ PM, E trđ MN )
⇒ KE//PN
a) CÓ PM //AB
=> CUNG AP= CUNG MB ( TÍNH CHẤT) (1)
MÀ CM ĐƯỢC B LÀ ĐIỂM CHÍNH GIỮA CUNG MN => CUNG MB=CUNG NB (2)
TỪ (1) (2) => CUNG AP= CUNG NB
b) CM ĐƯỢC KME=90 ĐỘ ( VÌ PM //AB MÀ AB VUÔNG GÓC MN )
VÌ I LÀ ĐIỂM CHÍNH GIỮA CUNG PM => OI VUÔNG GÓC PM TẠI K => OKM = 90 ĐỘ
TỨ GIÁC OKME CÓ OKM=KME=MEO=90 ĐỘ => TỨ GIÁC OKME LÀ HÌNH CHỮ NHẬT
c) CHỨNG MINH ĐƯỢC KE LÀ ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC PMN => KE // PN
MẶT KHÁC CÓ OK=ME=NE MÀ NE//OK (CÙNG VUÔNG GÓC AB )
=> TỨ GIÁC OKNE LÀ HÌNH BÌNH HÀNH => KE//ON
CÓ KE//ON MÀ KE//PN NÊN PN TRÙNG ON => O, P, N THẲNG HÀNG
Xem thêm câu trả lời
cho tam giác abc nội tiếp đường tròn đường kính ab. gọi I là điểm chính giữa cung nhỏ bc. trên đoạn ob lấy điểm m. tia im cắt đường tròn tâm o tại e, ce cắt ai tại K. qua m kẻ đường thẳng song song với ac cắt ce tại f. chứng minh mf=mb
Cho đường tròn tâm o dây ab, c là điểm nằm giữa cung ab. Điểm D thuộc tia đối của tia BA. Qua D kẻ đường thẳng song song BC cắt AC ở E. Qua điểm D kẻ đường thẳng song song AC cắt CB ở F a.Chứng minh tâm giác OCEtam giác OBFb.Chứng minh O,C,E,F thuộc đường tròn tâm O c.Gọi I là giao điểm của CD và EF Chứng minh O,O,I thẳng hàng d.Gọi K là giao điểm đường tròn tâm O và đường tròn tâm O chứng minh Góc CKD90độ
Đọc tiếp
Cho đường tròn tâm o dây ab, c là điểm nằm giữa cung ab. Điểm D thuộc tia đối của tia BA. Qua D kẻ đường thẳng song song BC cắt AC ở E. Qua điểm D kẻ đường thẳng song song AC cắt CB ở F
a.Chứng minh tâm giác OCE=tam giác OBF
b.Chứng minh O,C,E,F thuộc đường tròn tâm O'
c.Gọi I là giao điểm của CD và EF Chứng minh O,O',I thẳng hàng
d.Gọi K là giao điểm đường tròn tâm O và đường tròn tâm O' chứng minh Góc CKD=90độ
Cho nửa đường tròn tâm O, đường kính AB=2R, một dây cung MN=R di chuyển trên đường tròn. Qua M kẻ đường thẳng song song với ON cắt đường thẳng AB tại E. Qua N kẻ đường thẳng song song với Om cắt đường thẳng AB tại F. Gọi K là giao điểm của EN và FM. Hãy xác định của dây MN để chu vi tam giác MKN lớn nhất.
Cho đường tròn (O), dây AB, C là điểm chính giữa của cung AB. Điểm D thuộc tia đối của tia BA. Qua D kẻ đường thẳng song song với BC, cắt AC ở E. Qua D kẻ đường thẳng song song với AC cắt CB ở F.a) CM tam giác OCE tam giác OBFb) CM O,C,E,F cùng thuộc đường tròn (O)c) Gọi I là giao điểm của CD và EF. CM O,O:,I thẳng hàngd) Gọi K là giao điểm thứ hai của (O) với (O). CM góc CKD 90độ.
Đọc tiếp
Cho đường tròn (O), dây AB, C là điểm chính giữa của cung AB. Điểm D thuộc tia đối của tia BA. Qua D kẻ đường thẳng song song với BC, cắt AC ở E. Qua D kẻ đường thẳng song song với AC cắt CB ở F.
a) CM tam giác OCE = tam giác OBF
b) CM O,C,E,F cùng thuộc đường tròn (O')
c) Gọi I là giao điểm của CD và EF. CM O,O:,I thẳng hàng
d) Gọi K là giao điểm thứ hai của (O) với (O'). CM góc CKD= 90độ.
Cho nửa đường tròn [O;R] đường kính AB ; C là điểm chính giữa của cung AB . Lấy M thuộc cung nhỏ AC [M khác A và C] . Qua M kẻ tiếp tuyến d với nứa đường tròn , gọi H là giao điểm của BM và OC . Từ H kẻ đường song song với AB cắt d tại E
a, CM OHME là tứ giác nội tiếp
b, CM EH=R
a: C là điểm chính giữa của cung AB
=>OC vuông góc AB
góc OHE=góc OME=90 độ
=>OHME nội tiếp
b: góc AMB=1/2*sđ cung AB=90 độ
=>góc AMH+góc AOH=180 độ
=>OHMA nội tiếp
=>O,H,M,E,A cùng thuộc 1 đường tròn
=>góc EAO=90 độ
OHEA có 3 góc vuông
=>OHEA là hcn
=>EH=OA=R
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R và điểm M ở ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA, MB và cát tuyến MCD với đường tròn (O), trong đó điểm C ở giữa hai điểm M, D. Đường thẳng qua điểm C và vuông góc với OA cắt AB tại H. Gọi I là trung điểm của dây CD. Chứng minh HI song song với AD.
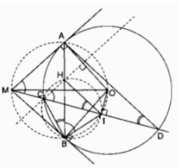

A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.

Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính EF. Lấy N, P thuộc EF sao cho ON=OP<R/2. Qua N kẻ đường thẳng vuông góc EF cắt (O) tại A và C. Qua P kẻ dây BD song song FC cắt AC tại M(B và O nằm khác phái so với AC). K là giao điểm OB và AC, Q là giao điểm EF và CD. Chứng minh KQ, BD, AO đồng quy
Ta có:
- Vì ON = OP < R/2, nên N và P nằm trong đường tròn tâm O, nên A, C, B, D đều nằm trên đường tròn (O).
- Vì AC // BD, nên theo định lí của dây cung, ta có: AM = MC và BM = MD.
- Ta có: ∠BAC = ∠BMC (do ABMC là hình bình hành) và ∠ACB = ∠AMB (do ABMC là hình bình hành).
- Vậy tứ giác ABMC là tứ giác cùng tứ giác nội tiếp, nên ta có: ∠BMC + ∠AMB = 180°.
- Từ đó, ta có: ∠BAC + ∠ACB = 180°.
- Vậy tứ giác ABCD là tứ giác điều hòa.
- Gọi K' là giao điểm của BD và AO. Ta cần chứng minh K', Q, A đồng quy.
- Ta có: ∠QAC = ∠QDC (do AC // BD) và ∠QCA = ∠QCB (do ABMC là hình bình hành).
- Vậy tứ giác AQCD là tứ giác cùng tứ giác nội tiếp, nên ta có: ∠QDC + ∠QCA = 180°.
- Từ đó, ta có: ∠QAC + ∠QCA = 180°.
- Vậy tứ giác AQCK' là tứ giác điều hòa.
- Vậy K', Q, A đồng quy. - Vậy KQ, BD, AO đồng quy.\
Xin tick!!
Đúng 0
Bình luận (0)
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếpb) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD MH.ANCâu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CACB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.a) C/m: MO...
Đọc tiếp
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.
a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếp
b) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD= MH.AN
Câu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CA=CB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.
a) C/m: MOCD là hình bình hành
b) Vẽ đường tròn tâm E bán kính EA cắt (O) tại điểm thứ 2 là N. Kẻ EF vuông góc với AC, EF cắt AN tại I, cắt (O) tại điểm thứ 2 là K; EB cắt AN tại H. C/m: BHIK nội tiếp.
Câu 3: Cho (O;R). Từ điểm S nằm ngoài đường tròn sao cho SO=2R. Vẽ tiếp tuyến SA,SB (A,B là tiếp tuyến). Vẽ cát tuyến SDE (D nằm giữa S và E), điểm O nằm trong góc ESB. Từ O kẻ đường vuông góc với OA cắt SB tại M. Gọi I là giao điểm của OS và (O).
a) C/m: MI là tiếp tuyến của (O)
b) Qua D kẻ đường vuông góc với OB cắt AB tại H và EB tại K. C/m: H là trung điểm của DK.

















