Bài 1 

Ta có : \(\frac{2x+2}{x^2-1}=0\)ĐK : \(x\ne\pm1\)

\(\Leftrightarrow2x+2=0\Leftrightarrow x=-1\)( ktm )

Bài 2 : 

Ta có : \(\frac{2x+3}{-x+5}=\frac{3}{4}\)ĐK : \(x\ne5\)

\(\Leftrightarrow8x+12=-3x+15\Leftrightarrow11x=3\Leftrightarrow x=\frac{3}{11}\)

Vậy phương trình có tập nghiệm là S = { 3/11 }

Phân thức 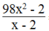 = 0 khi 98 x 2 + 2 = 0 và x – 2  ≠  0

Ta có: x – 2  ≠  0 ⇔ x  ≠  2

98 x 2 + 2 = 0  ⇔ 2 49 x 2 - 1 = 0 ⇔ (7x + 1)(7x – 1) = 0

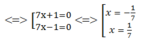
Ta có: 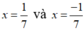 thỏa mãn điều kiện x  ≠  2

Vậy  thì phân thức  có giá trị bằng 0.

Phân thức 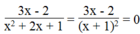 khi 3x – 2 = 0 và x + 1 2 ≠ 0

Ta có:  x + 1 2 ≠ 0  ⇔ x + 1 ≠ 0 ⇔ x ≠ - 1

3x – 2 = 0 ⇔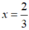 

Ta có: 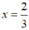 thỏa mãn điều kiện x ≠ - 1

Vậy 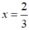 thì phân thức 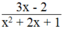có giá trị bằng 0.

Đặt phân thức đã cho là A 

\(ĐKXĐ:x^2-x\ne0\)\(\Leftrightarrow x\left(x-1\right)\ne0\)\(\Leftrightarrow\hept{\begin{cases}x\ne0\\x-1\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne1\end{cases}}\)

a) \(A=\frac{2x-2}{x^2-x}=\frac{2\left(x-1\right)}{x\left(x-1\right)}=\frac{2}{x}\)

Với \(x=3\)( thoả mãn ĐKXĐ ) \(\Rightarrow A=\frac{2}{3}\)

Với \(x=0\)( không khoả mãn ĐKXĐ ) \(\Rightarrow\)Không tìm được giá trị của A

b) \(A=2\)\(\Leftrightarrow\frac{2}{x}=2\)\(\Leftrightarrow x=1\)( không thoả mãn ĐKXĐ ) 

Vậy không tìm được giá trị của x để \(A=2\)

c) A có giá trị nguyên \(\Leftrightarrow\frac{2}{x}\inℤ\)\(\Leftrightarrow2⋮x\)\(\Leftrightarrow x\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)

So sánh với ĐKXĐ \(\Rightarrow x=1\)không thoả mãn

Vậy A nguyên \(\Leftrightarrow x\in\left\{-2;-1;2\right\}\)

ĐKXĐ:

----------->x khác 0        

---------->(x-1) khác 0 ----------> x khác 1

VẠY ĐKXĐ LÀ X khác 0 và 1.

Bạn tự rút gọn nha

a, 2x-2\ x^2-x=  2\x

Thay x=3 vào biểu thức có:

-----> = 2\3

Vậy nếu thay x=3 vào biểu thức thì = 2\3

thay x=0 vào biểu thức có

------> = 0 vì 2\0=0

VẬY nếu thay x=0 thì biểu thức thì =0

b,

theo đề bài ta có 

2\x=2

-----> 2:x=2

Vậy x=1 

Câu c mik ko chắc nên bn tự làm nha

mik rất sorry:(((((((

\(x^2-x=x\left(x-1\right)\)

Phân thức xác định khi: \(\Leftrightarrow x\left(x-1\right)\ne0\Leftrightarrow\hept{\begin{cases}x\ne0\\x-1\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne1\end{cases}}\)

ĐKXĐ: \(x\ne0,x\ne1\)

a) Ta có: \(A=\frac{2x-2}{x^2-x}=\frac{2\left(x-1\right)}{x\left(x-1\right)}=\frac{2}{x}\)

+) Với x = 3 

\(A=\frac{2}{3}\)

+) Với x = 0 (không tmđk) 

=> Loại

\(A=2\Rightarrow\frac{2}{x}=2\Rightarrow x=1\)(không tmđk)

\(\frac{x^2+2x}{2x+10}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}=\frac{x^2+2x}{2\left(x+5\right)}+\frac{x-5}{x}+\frac{50-5x}{2x\left(x+5\right)}=\)

\(=\frac{x\left(x^2+2x\right)+2\left(x+5\right)\left(x-5\right)+50-5x}{2x\left(x+5\right)}=\frac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}=\frac{x^3+4x^2-5x}{2x\left(x+5\right)}=\)

\(=\frac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\frac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\frac{x\left(x^2-1+4\left(x-1\right)\right)}{2x\left(x+5\right)}=\frac{x\left(x-1\right)\left(x+5\right)}{2x\left(x+5\right)}\)

a/ Để biểu thức xác đinh => 2x(x+5) khác 0 => x khác 0 và x khác -5

b/ Gọi biểu thức là A. Rút gọn A ta được: 

\(A=\frac{x\left(x-1\right)\left(x+5\right)}{2x\left(x+5\right)}=\frac{x-1}{2}\left(x\ne0;x\ne-5\right)\)

A=1 => x-1=2 => x=3

c/ A=-1/2 <=> x-1=-1 => x=0

d/ A=-3 <=> x-1=-6  => x=-5

a) ĐKXĐ: \(^{x^3+2x^2+x+2}\)khác 0

=> x^2(x+2)+(x+2) Khác 0

=> (x^2+1)(x+2) khác 0

=> x^2 khác -1(vô lý) và x khác -2

Vậy x khác -2 thì biểu thức A được xác định

b)\(A=\frac{3x^3+6x^2}{x^3+2x^2+x+2}=\frac{3x^2\left(x+2\right)}{x^2\left(x+2\right)+\left(x+2\right)}\)

\(=\frac{3x^2\left(x+2\right)}{\left(x^2+1\right)\left(x+2\right)}=\frac{3x^2}{x^2+1}\)

Để A=2 thì \(\frac{3x^2}{x+2}=2\)=>\(3x^2=2\left(x^2+1\right)=>3x^2=2x^2+2\)

\(=>x^2=2=>x=\sqrt{2}\)(Thỏa mãn điều kiện xác định)