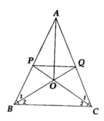
Gọi M,N,P là các thuộc cạnh BC,CA,AB của tam giác ABC cân tại A sao cho MNAP là hình bình hành. Gọi O là giao điểm của BN và CP. Chứng minh góc OMP= GÓC AMN.

Những câu hỏi liên quan
Cho các điểm M,N,P lần lượt thuộc các cạnh BC,CA,AB của tam giác ABC cân tại A sao cho MNAP là hình bình hành. Gọi O là giao điểm của CP và BN. Chứng minh \(\widehat{OMP}=\widehat{AMN}\)
Cho các điểm M, N, P theo thứ tự thuộc các cạnh BC, CA, AB của tam giác ABC cân tại A sao cho tứ giác MNAP là hình bình hành. Gọi O là giao điểm của BN và CP. Chứng minh \(\widehat{OMP}\)= \(\widehat{AMN}\)
Cho tam giác ABC. Xét các điểm M thuộc BC, N thuộc CA và P thuộc AB sao cho tứ giác APMN là một hình bình hành. Gọi O là giao điểm của các đường thẳng BN và CP. Xác định vị trí hình học của điểm M trên cạnh BC sao cho góc PMO= góc OMP
Gọi D là đỉnh thức tư của hình bình hành ABDC. Khi đó, O, M, D thẳng hàng.
Do giả thiết nên DB//MP, DC//MN. Từ đó, do O, M, D thẳng hàng, nên góc PMO = góc OMN <=> OM là phân giác góc PMN <=> DM là phân giác góc BDC
\(\Leftrightarrow\frac{MB}{MC}=\frac{DB}{DC}\)
Nhưng tứ giác ABDC là một hình bình hành nên BD = AC, CD = AB
do đó : \(\frac{DB}{DC}=\frac{AC}{AB}\)
Vì vậy :
góc PMO bằng góc OMN \(\Leftrightarrow\frac{MB}{MC}=\frac{AC}{AB}\)
Vậy với M là điểm trên cạnh BC sao cho \(\frac{MB}{MC}=\frac{AC}{AB}\) (hay M đối xứng với chân phân giác trong góc BAC qua trung điểm cạnh BC) thì góc PMO bằng góc OMN => Điều cần chứng minh
Đúng 1
Bình luận (2)
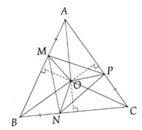
cho tam giác ABC cân tại A ,M là điểm bất kì trên BC .Từ M kẻ MN song song với AB,MP song song với AC (N THUỘC AC ,P thuộc AB
a)CM AQMN là hình bình hành
b)GỌI O LÀ GIAO CỦA BN VÀ CP ,Q là giao của MO và AB,K là giao của CP và MN .CM góc QMP=góc AMN
cho tam giác ABC cân tại A ,M là điểm bất kì trên BC .Từ M kẻ MN song song với AB,MP song song với AC (N THUỘC AC ,P thuộc AB
a)CM AQMN là hình bình hành
b)GỌI O LÀ GIAO CỦA BN VÀ CP ,Q là giao của MO và AB,K là giao của CP và MN .CM góc QMP=góc AMN
Cho các điểm M, N, P thứ tự thuộc các cạnh BC, CA, AB của tam giác ABC cân tại A sao cho tứ giác MNAP là hình bình hành. Gọi O là giao điểm của BN và CP. Chứng minh rằng góc ∠OMP = ∠AMN
1. Cho tam giác ABC (A=90 độ) (AB<AC), trên cạnh BC lấy N sao cho BN=NA, trên cạnh BC lấy M sao cho CM=CA. Tia phân giác góc ABC cắt AM tại E, tia phân giác góc ACB cắt AN tại D. Gọi O là giao của BE và CD, gọi H là giao của MD và NE.
a) Tính góc MAN
b) CHứng minh EODH là hình bình hành
c) Gọi K và I lần lượt là trung điểm của AH và MN. Chứng minh IEKD là hình vuông.
Cho tam giác ABC cân tại A. CP, BQ là các tia phân giác trong của tam giác ABC (P thuộc AB, Q thuộc AC). Gọi O là giao điểm của CP và BQ.a) Chứng minh tam giác OBC là tam giác cân.b) Chứng minh điểm O cách đều ba cạnh của tam giác ABC.c) Chứng minh đường thẳng AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.d) Chứng minh CP BQ.e) Tam giác APQ là tam giác gì? Vì sao?
Đọc tiếp
Cho tam giác ABC cân tại A. CP, BQ là các tia phân giác trong của tam giác ABC (P thuộc AB, Q thuộc AC). Gọi O là giao điểm của CP và BQ.
a) Chứng minh tam giác OBC là tam giác cân.
b) Chứng minh điểm O cách đều ba cạnh của tam giác ABC.
c) Chứng minh đường thẳng AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.
d) Chứng minh CP = BQ.
e) Tam giác APQ là tam giác gì? Vì sao?
Trên ba cạnh AB, BC và CA của tam giác đều ABC lấy các điểm theo thứ tự M, N, P sao cho AM BN CP. Gọi O là giao điểm ba đường trung trực của tam giác ABC.a) Tính số đo góc
M
A
O
^
.b) Chứng minh
∆
M
A
O
∆
O
P
C
.
c) Chứng minh O là giao điểm ba đường trung trực của tam giác MNP.
Đọc tiếp
Trên ba cạnh AB, BC và CA của tam giác đều ABC lấy các điểm theo thứ tự M, N, P sao cho AM = BN = CP. Gọi O là giao điểm ba đường trung trực của tam giác ABC.
a) Tính số đo góc M A O ^ .
b) Chứng minh ∆ M A O = ∆ O P C .
c) Chứng minh O là giao điểm ba đường trung trực của tam giác MNP.