cho tam giác ABC tại A .Vẽ BK,CI lần lượt vuông góc với AC,AB.Chứng minh BK=CI
HELP ME
Những câu hỏi liên quan
Cho tam giác abc cân tại a
a,Lấy e,d lần lượt là trung điểm ab và ac.cm bd=ce
b,vẽ bm,cn lần lượt là phân giác của góc b và góc c.cm bm=cn
c,vẽ bk,ci lần lượt vuông góc với ac và ab.cm bk=ci
Vẽ hình nha mình đang vội hứa mai sẽ tích
Cho tam giác đều ABC vuông cân tại A. Từ một điểm H trên BC vẽ đường thẳng vuông góc với BC cắt AB, AC lần lượt tại I, K. Cmr BK=CI.
Cho tam giác ABC vuông tại A. Từ một điểm H trên đường cạnh BC vẽ một đường thẳng vuông góc với BC cắt các đường thẳng AB, AC lần lượt tại I và K.a.Chứng minh BK = CI b.Gọi M, N, P, Q lần lượt là trung điểm của BC, CK, KI, IB. Chứng minh tứ giác MNPQ là hình vuông.
Cho tâm giác ABC nhọn , kẻ AH , BK , CI lần lượt vuông góc với AC , AB , BC .Chứng minh : a . AH AB+AC2��+��2b . AH +BK +CI AB +AC +BC
Đọc tiếp
Cho tâm giác ABC nhọn , kẻ AH , BK , CI lần lượt vuông góc với AC , AB , BC .Chứng minh :
a . AH <
b . AH +BK +CI < AB +AC +BC
a) \(AH\perp BC\) \(\Rightarrow AH< AB;AH< AC\)
\(\Rightarrow2.AH< AB+AC\Leftrightarrow AH< \dfrac{AB+AC}{2}\)
b) Theo câu a ta có: \(AH< \dfrac{AB+AC}{2}\) \(\left(1\right)\)
Tương tự ta có: \(BK< \dfrac{AB+BC}{2}\) \(\left(2\right)\)
\(CI< \dfrac{CA+CB}{2}\) \(\left(3\right)\)
Từ \(\left(1\right)\),\(\left(2\right)\) và \(\left(3\right)\) \(\Rightarrow AH+BK+CI< AB+AC+BC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại C. Vẽ AH vuông góc với BC, BK vuông góc với AC, biết AH giao với BK tại I. Chứng minh
a) AH = BK
b) CI là tia phân giác của góc ACB
c) Tia CI cắt AB tại D. Chứng minh CD là đường trung trực của AB
d) Biết AC = 20, CD = 16 .Tính chu vi của tam giác ABC
e) Chứng minh HD = 1/2 AB
Mọ người giúp em câu e ạ !! Cảm ơn rất nhiều ạ
e, Trên tia đối của tia DH lấy điểm F sao cho DF = DH = 1/2 FH
Xét tam giác ADF và BDH có :
AD = BD ( cmt )
ADF = BDH ( 2 góc đối đỉnh )
DF = DH ( cách vẽ )
=> Tam giác ADF = tam giác BDH ( c.g.c )
=> FH = AB ( 2 cạnh tương ứng )
Mà DF = DH = 1/2 FH ( cách vẽ )
=> HD = 1/2 AB ( đpcm )
Cho tam giác abc vuông tại. Từ H trên BC vẽ đường thẳng vuông góc với BC cắt AB và AC thứ tự tạ I và K
a) Chứng minh BK vuông góc với CI
b) Gọi M;N;P;Q lần lượt là trung điểm của BC;CK;KI;IB. C/m tứ giác MNPQ là hình vuông.
cho hình chữ nhật ABCD kẻ BK vuông góc với AC láy M,N lần lượt là trung điểm của AK,DC kẻ CI vuông góc với BM (I∈BM) và CI cắt BK tại E .cmr a,vẽ hình
b,EB=EK
c,tứ giác MNCE là hình bình hành
d,MN⊥BM
a: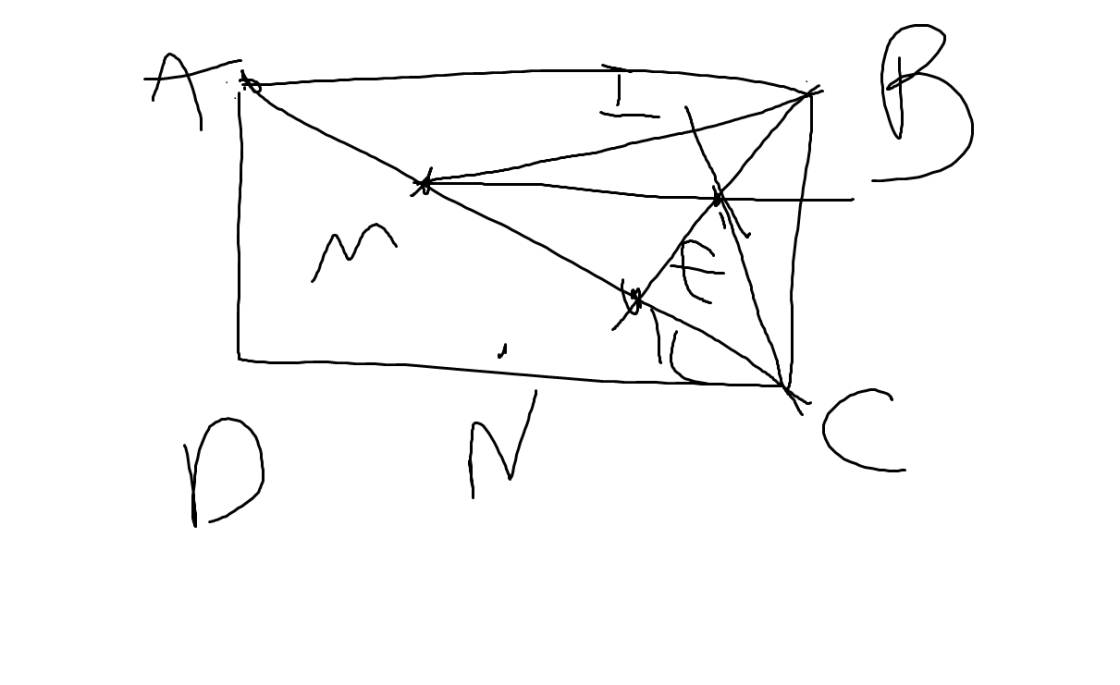 
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A (góc A <90), các đường cao AH, Bk , CI.
a, Tứ giác BIKC là hình gì ? tại sao?
b,Biết AB = 10cm: AC=12 cm. Tính BK và diện tích tam giác BIC
c, Kẻ đg vuông góc với AC ( E thuộc AE). Gọi M,N lần lượt là trung điểm của HE và CE. chứng minh AM vuông góc với HN
d, BC^2/AH^2=4EC/AE
Vẽ tam giác ABC nhọn . Trong tam giác ABC lấy điểm O . Vẽ OK sao cho vuông góc với AB, vẽ OI vuông góc với AC, vẽ OH vuông góc với BC . Chứng Minh AI^2+ BK^2+CH^2=AC^2+BH^2+CI^2