Cho tam giác ABC cân tại A. TRên các cạnh AB ; AC lần lượt lấy các điểm M và N sao cho AM + AN = AB. CHứng minh rằng: Khi M và N di chuyển trên AB và AC nhưng vẫn thỏa mãn AM + AN = AB thì đường trung trực của MN luôn đi qua một điểm cố định

Những câu hỏi liên quan
Cho tam giác ABC vuông cân tại A coa AB = AC = 10cm. Tam giác
vuông cân DEF nội tiếp tam giác ABC sao cho D,E,F lân lượt thuộc các cạnh
AB, BC, CA. Hãy xác định vị trí điểm D trên cạnh AB sao cho diện tích tam
giác DEF nhỏ nhất.
Cho tam giác ABC cân tại A . Trên cạnh AB lấy điểm E , trên cạnh AC lấy điểm F sao cho BE=CF a) CM tam giác AEF là tam giác cân b) tại trung điểm H của BE và tại trung điểm K của CF vẽ các đg trung trực của đoạn thẳng BE và CF , chúng cắt nhau tại O CMR tam giác AOH = AOK c) CM AO là đường phân giác của góc BAC , và cũng là đường chung trực của các đoạn thẳng EF , BC
Cho tam giác ABC cân tại A. Phân giác AH. Đường trunng trực của AB cắt AH tại O. Trên các cạnh AB và AC của tam giác lấy các điểm E và F sao cho AE+AF=AB. Chứng minh OE=OF
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
A. Hình thang.
B. Hình thang cân.
C. Hình thang vuông.
D. Cả A, B, C đều sai.
Đáp án cần chọn là: B
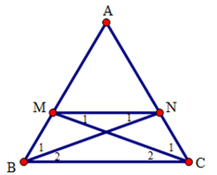
Ta có AB = AM + MB và AC = AN + NC
Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)
Suy ra AN = AM
Xét tam giác AMN cân tại A.
Suy ra A M N ^ = A N M ^ .
Xét tam giác ANM có: A ^ + A M N ^ + A N M ^ (tổng ba góc trong một tam giác)
A M N ^ = 180 0 − A 2 (vì A M N ^ = A N M ^ ) (1)
Xét tam giác ABC cân tại A ta có:
A ^ + B ^ + C ^ = 180 ° (tổng ba góc trong một tam giác) nên B ^ = 180 0 − A 2 (vì B ^ = C ^ ) (2)
Từ (1) và (2) A M N ^ = B ^
Mà B ^ , A M N ^ là hai góc đồng vị nên MN // BC
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có B ^ = C ^ (do ΔABC cân tại A) nên MNCB là hình thang cân.
Đúng 1
Bình luận (0)
cho tam giác ABC vuông cân tại A. Tia pg góc A cắt BC tại D, lấy điểm E trên cạnh AB, F trên cạnh AC sao cho AE=CF
CMR:a) tam giác ACB, tam giác ADC là tam giác vuông cân
b) tam giác CEF vuông cân
1)Cho tam giác ABC vuông cân tại A trên AB lấy D trên AC lấy E sao cho AD=AE qua D và A kẻ các đường thẳng vuông góc BE cắt BC tại I và K chứng minh IK=KC
2) cho tam giác ABC vuông tại A vẽ tam giác vuông cân DAB có cạnh huyền AB, E là trung điểm BC tính DE
Cho tam giác ABC cân tại A. Các tia phân giác của góc B và góc C cắt nhau tại O. Qua O kẻ đường thẳng song song với BC. Đường thẳng này cắt cạnh AB tại E và cắt cạnh AC tại F.
a) Tìm những tam giác cân có trên hình vẽ
b) Tìm những cặp tam giác cân bằng nhau
a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)
Có: ^OBC = ^OBA ( BF là phân giác ^B)
mà: ^EOB = ^OBC (cmt)
=> ^EOB = ^OBA => tam giác EBO cân tại E
Có: ^OCA = ^OCB ( BF là phân giác ^B)
mà: ^FOC = ^OCB (cmt)
=> ^FOC = ^OCA => tam giác FCO cân tại E
Ta có: ^AEF = ^B (cmt)
^AFE = ^C (cmt)
Mà ^B = ^C (tam giác ABC cân tại A)
=> ^AEF = ^AFE => tam giác AEF cân tại A
Có : ^ABF = ^CBF = \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)
^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)
mà : ^B = ^C (tam giác ABC cân tại A)
=> ^ACE = ^ABF = ^CBF = ^BCE
Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O
Xét tam giác FCO và tam giác EBO có:
^FOC = ^FOB ( đối đỉnh)
^FCO = ^EBO (^ABF = ^ACE)
OB = OC ( tg OBC cân tại O )
=> tam giác FCO = tam giác EBO(g-c-g)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông cân tại A.tia phân giác của góc A cắt BC tại D lấy điểm E trên cạnh AB,lấy điểm F trên cạnh AC sao cho AE = CF
chứng minh :
a) ADB , ADC là các tam giác vuông cân
b) DEF cũng là tam giác vuông cân
giúp mik nha !
Tính các góc của tam giác ABC cân tại A biết rằng trên cạnh AB có điểm D sao cho AB=DC=CB
Ta có: tam giác ABC cân tại A => góc ABC=góC ACB
DC=BC=AD => góC BAC=góc ACD
góc ABC=góC BDC
mà: góC BAC + gÓc ACD=góC BDC=góc ABC => 2.góc BAC=góc ABC
mặt khác: gÓc BAC + gÓC ABC + gÓc ACB=180 độ
=>góc BAC + 2.góc ABC=180 độ =>góc BAC + 2.2 góc BAC=180 độ=> 5.góc BAC=180 độ
=> góc BAC=36 độ
=> góc ABC=góc ACB=(180-36)/2=72 độ
k cho mình nha bạn ! Chúc bạn học tốt
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A, vẽ về phía ngoài tam giác ABC tam giác BCD vuông cân tại B. Gọi N là điểm bất kỳ trên cạnh BD. Trung trực của CN cắt AB tại M. Chứng minh tam giác CMN là tam giác vuông cân.

















