Cho tam giác ABC cân tại A.AM là phân giác của góc BAC.Từ M kẻ MH vuông góc với AB,kẻ MK vuông góc với AC.
a,CMR: AM vuông góc với BC
b,CMR: tam giác HMK là tam giác cân
c,CMR: HK//BC
d,Khi MH+MK=AM thì tam giác ABC đều.Hãy chứng minh điều đó
Những câu hỏi liên quan
cho tam giác ABC có AB = AC , kẻ AM vuông góc BC (M thuộc BC) a, CMR : tam giác AMB = tam giác AMC b, CMR : B = C và AM là phân giác của góc BAC c, kẻ MH , MK lần lượt vông góc với AB , AC . CMR : AH = AK
#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM` chung
`AB = AC (g``t)`
\(\widehat{AMB}=\widehat{AMC}=90^0\)
`=>` Tam giác `AMB =` Tam giác `AMC (ch-cgv)`
`b,` Vì Tam giác `AMB = ` Tam giác `AMC (a)`
`=>` \(\widehat{B}=\widehat{C}\) `(2` góc tương ứng `)`
`=>` \(\widehat{BAM}=\widehat{CAM}\) `( 2` góc tương ứng `)`
`=> AM` là tia phân giác của \(\widehat{BAC}\)
`c,` Xét Tam giác `AHM` và Tam giác `AKM` có:
`AM` chung
\(\widehat{HAM}=\widehat{KAM}(CMT)\)
`=>` Tam giác `AHM =` Tam giác `AKM (ch-gn)`
`=> AH = AK (2` cạnh tương ứng `)`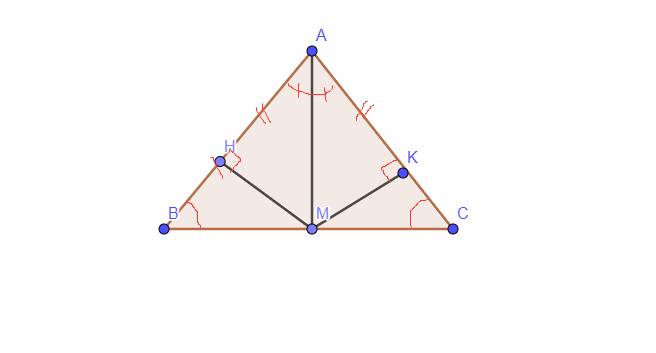
Đúng 3
Bình luận (0)
Cho Tam giác ABC cân tại A, (A90°) . Tia phân giác của góc A cắt cạnh BC tại M. Từ M kẻ MH vuông góc với AB , MK vuông góc vs ACa CM tam giác AMB tam giác AMCb CM AM vuông góc vs BCc CM MHMKd CM MA là tia phân giác của góc HMKe Qua A kẻ đường thẳng song song với BC cắt MH tại E, cắt MK tại F. CM tam giác MEF cânf gọi AM cắt HK tại I Tính AI biết AK5cm HK6cmGiúp mình với mình đang cần gấp.Cảm ơn
Đọc tiếp
Cho Tam giác ABC cân tại A, (A<90°) . Tia phân giác của góc A cắt cạnh BC tại M. Từ M kẻ MH vuông góc với AB , MK vuông góc vs AC
a CM tam giác AMB = tam giác AMC
b CM AM vuông góc vs BC
c CM MH=MK
d CM MA là tia phân giác của góc HMK
e Qua A kẻ đường thẳng song song với BC cắt MH tại E, cắt MK tại F. CM tam giác MEF cân
f gọi AM cắt HK tại I Tính AI biết AK=5cm HK=6cm
Giúp mình với mình đang cần gấp.Cảm ơn
Cho tam giác ABC có M là trung điiểm của BC, AM cũng là đường cao. Kẻ MH vuông góc với AB, MK vuông góc với AC. CMR :
a) Tam giác AMB = tam giác AMC
b) góc B = góc C
c) MH=MK
a/xét tg AMB và tg AMC:
góc AMB=góc AMC(=90 độ)
BM=CM(giả thiết)
AM:chung
\(\Rightarrow\)tg AMB=tg AMC(C-G-C)
b/Theo phần a ta có:tg AMB=tg AMC
\(\rightarrow\)góc B=góc C(2 góc tương ứng)
c/xét tg BHM và tg CKM:
góc B=góc C(theo phần b)
góc BHM=góc MKC=90 độ
BM=MC(gt)
\(\Rightarrow\)tg BHM= tg CKM(cạnh huyền-góc nhọn)
\(\rightarrow\)MH=MK(2 cạnh tương ứng)
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A .Gọi M là trung điểm của BC
a, Chứng minh AM vuông góc với BC
b , Chứng minh góc BAM = góc CAM
c, Kẻ MH vuông góc với AB tại H ; MK vuông góc với AC tại K chứng minh tam giác MHK cân tại M
d, Chứng minh tam giác AHK cân tại A
e, Chứng minh HK song song với BC
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường cao
nên AM là tia phân giác của góc BAC
hay góc BAM= góc CAM
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
hay ΔMHK cân tại M
d: Xét ΔAHK có AH=AK
nên ΔAHK cân tại A
e: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A và M là trung điểm BC. CMR:
a) Tam giác ABM = Tam giác ACM
b) Từ M vẽ MH vuông góc với AB, MK vuông góc với AC. CMR: BH = CK
c) Từ B kẻ BP vuông góc với AC, BP cắt MH tại I. CMR: tam giác IBM cân
cho tam giác abc cân tại a gọi m là trung điểm của bc kẻ MH vuông góc với AB tại H. MK vuông góc với AC tại K
CMR a) tam giác MHB=tam giác MKC
b) tam giác AMH= tam giác AMK
C) AM vuông góc vs BC
GIÚP MÌNH VỚI MÌNH CẦN GẤP
a, xét tam giác MBH và tam giác MCK ta có:
góc MHB= góc MKC=90 độ
BM=MC(gt)
góc B =góc C(gt)
vậy tam giác BMH = tam giác CMK(ch-gn)
Đúng 0
Bình luận (0)
b, xét tam giác AMH và tam giác AMK có:
AM chung
MH=MK( do tam giác BMH= tam giác CMK)
góc AHM= góc AKM=90 độ
suy ra tam giác AMH= tam giác AMK( ch-cgv)
Đúng 0
Bình luận (0)
ta có: góc AMH= góc AMK( tam giác AMH= tam giac AMK)
góc BMH= góc CMK( do 2 tam giác câu a bằng nhau)
suy ra góc AMH+ góc BMH= góc AMK+ góc CMK
mà góc BMH+góc HMA+ góc AMk+ góc CMK= 180 độ
suy ra góc AMH+ góc BMH= góc AMK+ góc CMK=180 độ chia 2=90 độ
suy ra AM vuông góc với BC( đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Kẻ AM vuông góc với BC tại M. Gọi E là một điểm nằm giữa M và C. Kẻ BH, CK vuông góc AE tại H và K. CMR: MH = MK
bạn trên làm đúng rồi đó chắc chắn 100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000%
Đúng 0
Bình luận (0)
Cho tám giác ABC vuông tại A . lấy điểm M là trung điểm của BC . Chứng minh tam giác abm = tam giác acm. Kẻ MH vuông góc với AB tại H. MK vuông góc với AC tại K. Chứng minh HK vuông góc với AM
Xem chi tiết
Nếu tam giác ABC mà vuông tại A thì 2 tam giác ABM và ACM không thể bằng nhau đc
Mk nghĩ bn nên xem lại đề bài.
Cho tam giác ABC vuông tại A và AB=AC. Qua A vẽ đường thẳng xy sao cho B và C nằm cùng phía với xy.
a)CMR: tam giác AHB=tam giác CKA
b)CMR: HK = BH+CK
c)Gọi M là trung điểm của BC. CMR: AM vuông góc BC và AM là phân giác của góc BAC, AM = \(\frac{1}{2}\) BC.
d) CMR: MHK vuông góc tại M, MH=MK