cho hình bình hành ABCD.Gọi M là trung điểm của AB,N là trùn điểm của DC.Chứng minh rằng AN=CM

Những câu hỏi liên quan
cho hình bình hành ABCD có M,N là trung điểm của AB và CD , AN và CM căt sBD ở E và F . Chứng minh :
a) AM=CN và tứ giác AMCN là hình bình hành
b) F là trung điểm của BE và E là trùn điểm của DF
Cho hình bình hành ABCD.Gọi M,N theo thứ tư là trung điểm của AB và CD.Gọi I là giao điểm của MN và AN,K là giao điểm của MC và BN Chứng minh rằng a,MINK là hình bình hành b,Các đường thẳng A ,MN,IK đồng quy
Cho hình bình hành ABCD.Gọi M,N,E,F theo thứ tự là trung điểm của BC, AN, AB, CD
Hãy chứng minh: MNEF la hình bình hành.
Cho hình bình hành ABCD.gọi M,N lần lượt là trung điểm của các cạnh AB,DC
a, Tứ giác AMCN là hình gì .Tại sao
b, Gọi E,Flaanf lượt là giao điểm của BD với AN và CM. Chứng minh DE=ÈF=FB
cho hình bình hành ABCD.gọi E và F theo thứ tự là trung điểm của AB và CD
a )chứng minh rằng AF // CE
b) Gọi M , N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN =NB
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
Đúng 2
Bình luận (0)
cho hình bình hành ABCD.gọi E và F theo thứ tự là trung điểm của AB và CD
a )chứng minh rằng AF // CE
b) Gọi M , N theo thứ tự là giao điểm của BD và AF, CE. Chứng minh rằng DM = MN =NB
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
Đúng 1
Bình luận (0)
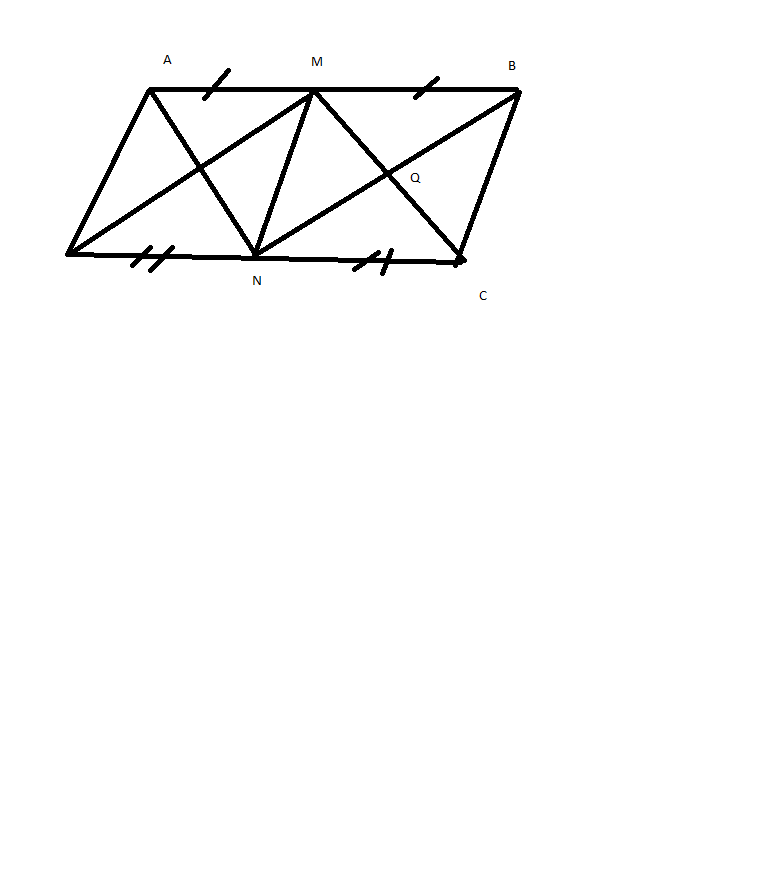
Câu 15 (3,5 điểm): Cho hình bình hành ABCD có cạnh AB = 2 AD Gọi M, N lần lượt là trung điểm của AB và CD.
Chứng minh rằng :
a) Tam giác ADN cân.
b) AN là phân giác của góc BAD.
c) Gọi giao điểm của AN với DM là P, CM với BN là Q. Chứng minh PMQN là hình chữ nhật
a) Vì ABCD là hình bình hành nên
AB=CD=2a, AD=BC=a
ta có: M,N là trung điểm của AB và CD
=> DN=1/2CD=a
=> AD=DN
Vậy tam giác ADN cân tại D(đpcm)
=> DAN=DNA
b) Ta có: AB//CD => AND=MAN(So le trong)
=> DAN=MAN
=>AN là tia phân giác của góc BAD
Đúng 0
Bình luận (0)
c) Chứng minh tương tự câu B ta được:
AMCN là hình bình hành (vì AM//CN, AM=CN)
=>AN//CM=> PN//MQ
Ta có: BMND là hình bình hành (chứng minh b)
=>DM//BN => MP//NQ
=> MPNQ là hình bình hành(1)
Ta có: AM//DN,AM=DN=a
=> AMND là hình bình hành
mặt khác AD=AN(chứng minh a)
=>AMND là hình thoi
=> AN vuông góc với DM(tính chất 2 đường chéo của hình thoi)
=> MPN= 90 độ (2)
Từ (1) và (2) suy ra PMQN là hình chữ nhật ( dấu hiệu: hbh có 1 góc vuông là hcn)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình bình hành ABCD có AB = 2AD.Gọi M, N lần lượt là trung điểm của AB và CD. a) Chứng minh rằng : tứ giác amcn là hình bình hành , tứ giác amnd là hình gì b) Gọi I là giao điểm của AN và DM , K là giao điểm BN và CM . Tứ giác MINK hình gì c) Chứng Minh : IK // CD
Xem chi tiết
a: Xét tứ giác AMCN có
AM//CN
AM=CN
=>AMCN là hình bình hành
Xét tứ giác AMND có
AM//ND
AM=ND
AM=AD
=>AMND là hình thoi
b: AMND là hình thoi
=>I là trung điểm chung của AN và MD và AN vuông góc MD tại N
Xét tứ giác MBCN có
MB//CN
MB=CN
MB=BC
=>MBCN là hình thoi
=>MC vuông góc BN tại K và K là trung điểm chung của MC và BN
Xét ΔMDC có
MN là trung tuyến
MN=DC/2
=>ΔMDC vuông tại M
Xét tứ giác MINK có
góc MIN=góc MKN=góc IMK=90 độ
=>MINK là hình chữ nhật
c: Xét ΔMDC có MI/MD=MK/MC
nên IK//DC
Đúng 0
Bình luận (0)
cho hình bình hành abcd.gọi m,n,i,k theo thứ tự là trung điểm của ab,bc,cd,da.gọi giao điểm của AI với kb,dn theo thứ tự là e,h. họi giao điểm của cm với kb ,dn theo thứ tự là f,g.chứng minh rằng : a, ae=eh=gc. b, Segh=1/5Sabcd