Cho Tam giác ABC nhọn với H là trực tâm. Chứng minh rằng \(\widehat{BAC}+\widehat{BHC}=180^0\)
Mong mọi người giúp đỡ ạ, e cảm ơn rất nhiều!
Q:Cho tam giác nhọn ABC, H là trực tâm. Gọi D là điểm đối xứng với H qua BC .Chứng minh: a)Tam giác HBC=Tam giác DBC b) Góc BAC + góc BDC =180° Làm giúp mik với , mik đang cần gấp ạ , làm ơn🥺
a: Ta có: H và D đối xứng nhau qua BC
nên BC là đường trung trực của HD
Suy ra: BH=BD và CH=CD
Xét ΔHBC và ΔDBC có
BH=BD
BC chung
HC=DC
Do đó: ΔHBC=ΔDBC
Bài 1:Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AC. I là trung điểm HE. AI cắt BC tại M. Chứng minh rằng EH là phân giác của \(\widehat{BEM}\) .
Bài 2: Cho tam giác nhọn ABC với trực tâm H. Một điểm M nằm trong tam giác thỏa mãn \(\widehat{MBA}=\widehat{MCA}\). Gọi E, F lần lượt là hình chiếu vuông góc của M trên AC, AB. I, J lần lượt là trung điểm của BC, MA. CMR: IJ, MH, EF đồng quy.
Mọi người giúp mik với, thứ 3 phải nộp rồi ạ
cho tam giác \(ABC\) nhọn \(H\) là trực tâm của tam giác đó. biết rằng \(AH=BC\). tính số đo góc \(\widehat{BAC}\)
Giải dùm mình với ạ. mơn nhiều
H là trực tâm hay đường cao???
Nếu là trực tâm thì không làm được đâu :)
BÂY GIỜ CÓ BẠN NÀO ONLINE HỌC GIỎI HÌNH GIÚP MÌNH VỚI:
Cho tam giác ABC có trực tâm H. M là điểm nằm trong tam giác sao cho ∠ABM = ∠ACM. Kẻ ME ⊥ AC, MF ⊥ AB. Gọi K là trực tâm tam giác AEF. Chứng minh rằng K, M, H thẳng hàng.
MÌNH CẦN GẤP Ạ. CẢM ƠN MỌI NGƯỜI
Cho tam giác ABC có AH là đường cao, gọi D và E lần lượt là hình chiếu của H trên AB và AC. Chúng minh rằng;
a, tam giác ABH đồng dạng với tam giác AHD
b, He2= AE.AC
Mọi người giúp mình với ạ. Cảm ơn mọi người rất nhiều!
a, Xét △ABH và △AHD có:
∠AHB=∠ADH (=90o) , ∠BAH chung
⇒ △ABH ∼ △AHD (g.g)
b, Xét △AHE và △HCE có:
∠AHE=∠ACH (cùng phụ ∠AHC), ∠AEH=∠CEH (=90o)
⇒ △AHE ∼ △HCE (g.g)
⇒ HEEC=AEHEHEEC=AEHE ⇒ HE2=AE.EC
cho tam giác nhọn abc,trực tâm h.Gọi k là điểm đối xứng với h qua bc.
a)chứng minh tam giác bhc và bkc bằng nhau
b)cho góc bac=70 độ .Tính số đo góc bkc
a: Ta có: H và K đối xứng nhau qua BC
nên BC là đường trung trực của HK
Suy ra: BH=BK và CH=CK
Xét ΔBHC và ΔBKC có
BH=BK
BC chung
HC=KC
Do đó: ΔBHC=ΔBKC
cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R). Gọi H là trực tâm của tam giác ABC. AH kéo dài cắt đường tròn (O;R) tại D:
a, Chứng minh rằng\(\widehat{BAH}=\widehat{CAO}\)
b, Giả sử AH=R. Chứng minh rằng: \(\widehat{BAC}=60^o\)
c, Tính tổng: \(^{AB^2+BD^2+DC^2+CA^2}\)theo R
Cho tam giác ABC có \(\widehat A = {100^0}\) và trực tâm H. Tìm góc BHC.
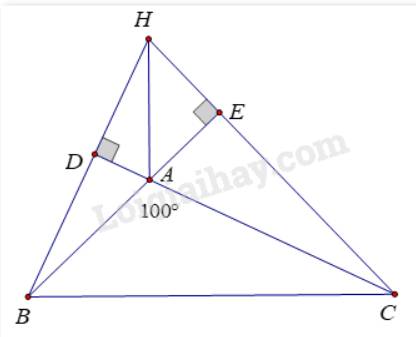
Gọi E là chân đường cao từ C xuống AB, D là chân đường cao từ B xuống AC
=> HC ⊥ BE, HB ⊥ CD
Ta có: Vì \(\widehat {BAC}\) và \(\widehat {BAD}\) là 2 góc kề bù nên
\(\begin{array}{l}\widehat {BAC} + \widehat {BAD} = {180^0}\\ \Rightarrow {100^0} + \widehat {BAD} = {180^0}\\ \Rightarrow \widehat {BAD} = {180^0} - {100^0}\\ \Rightarrow \widehat {BAD} = {80^0}\end{array}\)
∆ ADB là tam giác vuông tại D:
\(\begin{array}{l}\widehat {BAD} + \widehat {ABD} = {90^0}\\ \Rightarrow {80^0} + \widehat {ABD} = {90^0}\\ \Rightarrow \widehat {ABD} = {10^0}\end{array}\)
∆ BEH là tam giác vuông tại E
\(\begin{array}{l}\widehat {EBH} + \widehat {BHE} = {90^0}\\ \Rightarrow {10^0} + \widehat {BHE} = {90^0}\\ \Rightarrow \widehat {BHE} = {80^0}\end{array}\)
Hay \(\widehat {BHC} = {80^0}\)
Cho tam giác ABC nhọn. Có H là trực tâm của tam giác. Chứng minh: AB + AC > AH + BH + CH
Giải giúp cảm ơn nhiều !!!!!!!!!!!!!!!!!!!!
thiếu đề nhưng mk đã làm 1 bài giống thế này nên biết đoạn sau của nó như sau: CMR:AB+BC+CA>3/2(AH+BH+CH)...Nếu ko đúng thì bỏ qua nhé!
Nếu chỉ có BDT đươn thuần thì :
Qua H kẻ đt // AC cắt AB tại X và đt // AB cắt AC tại Y => XHY là hbh và HX vg BH, HY vg CH
AB + AC = BX + (XA + AY) + YC = BX + (AX + XH) + YC > HB + HA + HC
Tương tự có BA + BC > HA + HB + HC, CA + CB > HA + HB + HC
Cộng vế theo vế 3 bđt ta có 2(AB + AC + BC) > 3(HA + HB + HC)
```````````````````````````````````````...
Ta se Cm một BDT mạnh hơn và toàn diện hơn
Giả sử a >=b >= c. Do 2S = a ha = b hb = c hc =>ha <= hb <= hc
Goij A1; B1 ; C1 lan luot la hinh chieu cua A; B : C len cac canh cua Tam giac ABC
Ta co ha = AH.S/( Sb + Sc) ≤ hb = BH.S/(Sa + Sc) => AH( Sa + Sc) ≤ BH( Sb + Sc) (1 )
Ta se CM Sa ≥ Sb
DO Sa/Sb = BC1/AC1 = BC cosB /( AC cosA) = sinA cosB/(sinB cosA) = tanA/tanB ≥ 1 do a ≥ b suy ra Sa≥ Sb => Sa + Sc ≥ Sb + Sc ( 2)
Tu (1) va (2 ) suy ra AH ≤ BH, tuong tu ta suy ra BH ≤ CH do do AH ≤ BH ≤ CH \
Do 6S = a ha + b hb + c hc = aAH + b BH + c CH + 2(Sa+Sb+Sc) =
= aAH + b BH + c CH +2S => aAH + b BH + c CH = 4S
Áp dụng BDT che-bu-sep ta co (a+b+c)(AH + BH + CH) <= 3( a AH + b BH + c CH)
= 12S = 6absinC = 24R^2 sinA sinB sinC
Ta dự đoán 12R^2 sinA sinB sinC <= 1/(2√3) (a+b+c)^2 = 2/(√3)R^2 * ( sinA + sinB + sinC)^2
<=> sinA sinB sinC < = 1/(6√3) ( sinA + sinB + sinC)^2
Ta có (sinA + sinB + sinC )^2 <= 3( sin^2A + sin^2B + sin^2C) =
= 3/2 ( 2 - cos^2C + cosC cos( A-B) ) <= 3/2 ( 2 -cos^2C + cosC)
<= 27/4 =>sinA + sinB + sinC ≤ 3√3/2
=> 3√3/2 ≥ 3³√(sinA sinB sinC) => ³√(sinA sinB sinC) ≤ √3/2
suy ra (sinA + sinB + sinC)²/(sinA sinB sinC) ≥ 9/³√(sinA sinB sinC) ≥ 6√3
Từ đó suy ra (a+b+c)(AH + BH + CH) ≤ √3/3 ( a + b + c )² =>
=> 3/2( AH + BH + CH) ≤ √3/2 (a+b+c) < a + b + c
THIẾU ĐỀ NHƯNG MÌNH LÀM BÀI TƯƠNG TỰ GIỐNG BÀI CỦA BẠN NHA !
Nếu chỉ có BDT đươn thuần thì :
Qua H kẻ đt // AC cắt AB tại X và đt // AB cắt AC tại Y => XHY là hbh và HX vg BH, HY vg CH
AB + AC = BX + (XA + AY) + YC = BX + (AX + XH) + YC > HB + HA + HC
Tương tự có BA + BC > HA + HB + HC, CA + CB > HA + HB + HC
Cộng vế theo vế 3 bđt ta có 2(AB + AC + BC) > 3(HA + HB + HC)
```````````````````````````````````````...
Ta se Cm một BDT mạnh hơn và toàn diện hơn
Giả sử a >=b >= c. Do 2S = a ha = b hb = c hc =>ha <= hb <= hc
Goij A1; B1 ; C1 lan luot la hinh chieu cua A; B : C len cac canh cua Tam giac ABC
Ta co ha = AH.S/( Sb + Sc) ≤ hb = BH.S/(Sa + Sc) => AH( Sa + Sc) ≤ BH( Sb + Sc) (1 )
Ta se CM Sa ≥ Sb
DO Sa/Sb = BC1/AC1 = BC cosB /( AC cosA) = sinA cosB/(sinB cosA) = tanA/tanB ≥ 1 do a ≥ b suy ra Sa≥ Sb => Sa + Sc ≥ Sb + Sc ( 2)
Tu (1) va (2 ) suy ra AH ≤ BH, tuong tu ta suy ra BH ≤ CH do do AH ≤ BH ≤ CH \
Do 6S = a ha + b hb + c hc = aAH + b BH + c CH + 2(Sa+Sb+Sc) =
= aAH + b BH + c CH +2S => aAH + b BH + c CH = 4S
Áp dụng BDT che-bu-sep ta co (a+b+c)(AH + BH + CH) <= 3( a AH + b BH + c CH)
= 12S = 6absinC = 24R^2 sinA sinB sinC
Ta dự đoán 12R^2 sinA sinB sinC <= 1/(2√3) (a+b+c)^2 = 2/(√3)R^2 * ( sinA + sinB + sinC)^2
<=> sinA sinB sinC < = 1/(6√3) ( sinA + sinB + sinC)^2
Ta có (sinA + sinB + sinC )^2 <= 3( sin^2A + sin^2B + sin^2C) =
= 3/2 ( 2 - cos^2C + cosC cos( A-B) ) <= 3/2 ( 2 -cos^2C + cosC)
<= 27/4 =>sinA + sinB + sinC ≤ 3√3/2
=> 3√3/2 ≥ 3³√(sinA sinB sinC) => ³√(sinA sinB sinC) ≤ √3/2
suy ra (sinA + sinB + sinC)²/(sinA sinB sinC) ≥ 9/³√(sinA sinB sinC) ≥ 6√3
Từ đó suy ra (a+b+c)(AH + BH + CH) ≤ √3/3 ( a + b + c )² =>
=> 3/2( AH + BH + CH) ≤ √3/2 (a+b+c) < a + b + c
```````````````````````````````````````...
Rõ ràng BDT cuối mà ta cm dc mạnh hơn BDT cần CM
Nếu chỉ có BDT đươn thuần thì :
Qua H kẻ đt // AC cắt AB tại X và đt // AB cắt AC tại Y => XHY là hbh và HX vg BH, HY vg CH
AB + AC = BX + (XA + AY) + YC = BX + (AX + XH) + YC > HB + HA + HC
Tương tự có BA + BC > HA + HB + HC, CA + CB > HA + HB + HC
Cộng vế theo vế 3 bđt ta có 2(AB + AC + BC) > 3(HA + HB + HC)
```````````````````````````````````````...
Ta se Cm một BDT mạnh hơn và toàn diện hơn
Giả sử a >=b >= c. Do 2S = a ha = b hb = c hc =>ha <= hb <= hc
Goij A1; B1 ; C1 lan luot la hinh chieu cua A; B : C len cac canh cua Tam giac ABC
Ta co ha = AH.S/( Sb + Sc) ≤ hb = BH.S/(Sa + Sc) => AH( Sa + Sc) ≤ BH( Sb + Sc) (1 )
Ta se CM Sa ≥ Sb
DO Sa/Sb = BC1/AC1 = BC cosB /( AC cosA) = sinA cosB/(sinB cosA) = tanA/tanB ≥ 1 do a ≥ b suy ra Sa≥ Sb => Sa + Sc ≥ Sb + Sc ( 2)
Tu (1) va (2 ) suy ra AH ≤ BH, tuong tu ta suy ra BH ≤ CH do do AH ≤ BH ≤ CH \
Do 6S = a ha + b hb + c hc = aAH + b BH + c CH + 2(Sa+Sb+Sc) =
= aAH + b BH + c CH +2S => aAH + b BH + c CH = 4S
Áp dụng BDT che-bu-sep ta co (a+b+c)(AH + BH + CH) <= 3( a AH + b BH + c CH)
= 12S = 6absinC = 24R^2 sinA sinB sinC
Ta dự đoán 12R^2 sinA sinB sinC <= 1/(2√3) (a+b+c)^2 = 2/(√3)R^2 * ( sinA + sinB + sinC)^2
<=> sinA sinB sinC < = 1/(6√3) ( sinA + sinB + sinC)^2
Ta có (sinA + sinB + sinC )^2 <= 3( sin^2A + sin^2B + sin^2C) =
= 3/2 ( 2 - cos^2C + cosC cos( A-B) ) <= 3/2 ( 2 -cos^2C + cosC)
<= 27/4 =>sinA + sinB + sinC ≤ 3√3/2
=> 3√3/2 ≥ 3³√(sinA sinB sinC) => ³√(sinA sinB sinC) ≤ √3/2
suy ra (sinA + sinB + sinC)²/(sinA sinB sinC) ≥ 9/³√(sinA sinB sinC) ≥ 6√3
Từ đó suy ra (a+b+c)(AH + BH + CH) ≤ √3/3 ( a + b + c )² =>
=> 3/2( AH + BH + CH) ≤ √3/2 (a+b+c) < a + b + c