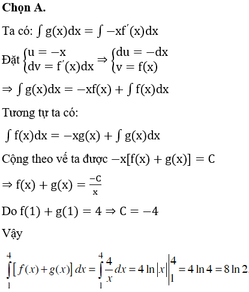Cho hàm số f(x) thỏa mãn x.f(x+2)=(x2-9). f(x).Tính f(5)

Những câu hỏi liên quan
cho đa thức f(x) xác định với mọi x thỏa mãn
x.f(x+2) =( x2
-9).f(x)
1) tính f(5)
2) chứngminh rằng f(x) có ít nhất 3 nghiệm
\(a,f\left(5\right)\Rightarrow x=3\\ 3f\left(5\right)=0f\left(3\right)\Rightarrow f\left(5\right)=0\\ b,x=0\Rightarrow0f\left(2\right)=-9f\left(0\right)\Rightarrow f\left(0\right)=0\)
=> x = 0 là nghiệm
\(x=-3\Rightarrow-3f\left(-1\right)=\left(9-9\right)f\left(-3\right)=0f\left(-3\right)\\ \Rightarrow f\left(-1\right)=0\)
=> x = -1 là nghiệm
Theo ý a) ta có \(x=5\)
\(\Rightarrow f\left(x\right)\) có 3 nghiệm \(=\left\{0;-1;5\right\}\)
Đúng 3
Bình luận (0)
Cho hàm số y=f(x) thỏa mãn: 2.f(x)-x.f(x)=x+10(với mọi x thuộc R).Tính f(2).
cho hàm số y =f(x) thỏa mãn x.f(x)+f(\(\frac{1}{x}\)) =2x+1.Tính f(2)
Cho hàm số y f(x) thỏa mãn
∫
0
π
2
sin
x
.
f
(
x
)
d
x
f
(
0
)
1
. Tính
I
∫
0
π
2
cos
x
.
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) thỏa mãn ∫ 0 π 2 sin x . f ( x ) d x = f ( 0 ) = 1 . Tính I = ∫ 0 π 2 cos x . f ' ( x ) d x
A. I=1.
B. I=0.
C. I=2.
D. I=-1.
Cho hàm số x thỏa mãn 2.f(x)-x.f(-x)=x + 10 với mọi x . Vậy f(2) bằng?
ap dung ta co:
f(2)=2f(2)-2f(-2)=12 (1)
f(-2)=2f(-2)+2f(2)=8 (2)
cong tung ve cua (1) va(2) ta co:
4f(2)=20
=>f(2)=5
Đúng 1
Bình luận (0)
Cho hàm số f(x) và g(x) có đạo hàm trên đoạn [1;4] và thỏa mãn hệ thức:
f
(
1
)
+
g
(
1
)
4
g
(
x...
Đọc tiếp
Cho hàm số f(x) và g(x) có đạo hàm trên đoạn [1;4] và thỏa mãn hệ thức: f ( 1 ) + g ( 1 ) = 4 g ( x ) = - x . f ' ( x ) ; f ( x ) = - x . g ' ( x ) . Tính tích phân ∫ 1 4 [ f ( x ) + g ( x ) ] dx
A. 8ln2.
B. 3ln2
C. 6ln2
D. 4ln2
cho đa thức f(x) xác định với mọi x thỏa mãn
x.f(x+2) =( x\(^2\)-9).f(x)
1) tính f(5)
2) chứngminh rằng f(x) có ít nhất 3 nghiệm
1) Xét với x=3x=3 thì : 3.f(5)=(32−9).f(3)3.f(5)=(32−9).f(3)
⇒3.f(5)=0⇒f(5)=0⇒3.f(5)=0⇒f(5)=0 (*)
2) Xét với x=0⇔0=−9.f(0)⇒f(0)=0x=0⇔0=−9.f(0)⇒f(0)=0
nên x=0x=0 là 1 nghiệm của đa thức f(x)f(x) (1)
Xét với x=−3⇔3.f(−1)=0⇒f(−1)=0x=−3⇔3.f(−1)=0⇒f(−1)=0
nên x=−1x=−1 là 1 nghiệm của đa thức f(x)f(x) (2)
Từ (*)(1)(2) ⇒⇒ f(x)f(x) có ít nhất 3 nghiệm.
Đúng 0
Bình luận (1)
1) Xét với x=3x=3 thì : 3.f(5)=(32−9).f(3)3.f(5)=(32−9).f(3)
⇒3.f(5)=0⇒f(5)=0⇒3.f(5)=0⇒f(5)=0 (*)
2) Xét với x=0⇔0=−9.f(0)⇒f(0)=0x=0⇔0=−9.f(0)⇒f(0)=0
nên x=0x=0 là 1 nghiệm của đa thức f(x)f(x) (1)
Xét với x=−3⇔3.f(−1)=0⇒f(−1)=0x=−3⇔3.f(−1)=0⇒f(−1)=0
nên x=−1x=−1 là 1 nghiệm của đa thức f(x)f(x) (2)
Từ (*)(1)(2) ⇒⇒ f(x)f(x) có ít nhất 3 nghiệm.
Đúng 0
Bình luận (1)
cho hàm số y=f(x) thỏa mãn f(x)-x.f(-x)=x+1 với mọi x thuộc Rtính f(1)
Cho hàm số f(x) xác định với mọi x thuộc R và thỏa mãn tính chất
(1-x^2).f(x)=x.f(x+1)
nhanh lên nha