chứng minh rằng :
nếu 0 < x <1 thì căn của x > x
Những câu hỏi liên quan
Chứng minh rằng f′(x) > 0 ∀x ∈ R, nếu f ( x ) = 2 x + sin x
Chứng minh rằng nếu x>0 thì 1/x - 1/(x+1)>0
ơi STN = số thứ nhất
STH = SỐ THỨ 2 NHÉ
STB = SỐ THỨ 3 NHA
Chứng minh rằng nếu \(x>0\)thì \(\frac{1}{x}-\frac{1}{x+1}>0\):
Ta có : \(\frac{1}{x}-\frac{1}{x+1}>0\Rightarrow\frac{1}{x}>\frac{1}{x+1}\)
\(\Rightarrow x+1>x\)(đúng)
Học tốt
Chứng minh rằng hàm số:
f
x
x
-
1
2
n
ế
u
x
≥
0...
Đọc tiếp
Chứng minh rằng hàm số:
f x = x - 1 2 n ế u x ≥ 0 - x 2 n ế u x < 0
Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2 .
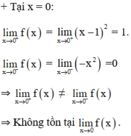
⇒ Không tồn tại đạo hàm của f(x) tại x = 0.
Đúng 0
Bình luận (0)
Chứng minh rằng f′(x) 0 ∀x ∈ R , nếu:
f
(
x
)
cos
6
x
+
2
sin
4
x
.
cos
2
x
+
3
sin
2
x
.
cos
4
x
+
...
Đọc tiếp
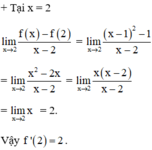
Chứng minh rằng f′(x) = 0 ∀x ∈ R , nếu: f ( x ) = cos 6 x + 2 sin 4 x . cos 2 x + 3 sin 2 x . cos 4 x + sin 4 x
Chứng minh các biểu thức đã cho không phụ thuộc vào x.
f(x) = 1 ⇒ f′(x) = 0
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số:
f
x
-
2
x
nếu
x
≥
0
sin...
Đọc tiếp
Chứng minh rằng hàm số:
f x = - 2 x nếu x ≥ 0 sin x 2 nếu x < 0
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
Hàm số:
f
x
=
-
2
x
nếu
x
≥
0
sin
x
2
nếu
x
<
0
Không có đạo hàm tại x = 0 vì:
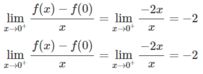
Mặt khác, với x < 0 thì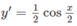 
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
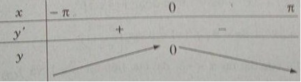
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y CD = y(0) = 0.
Đúng 0
Bình luận (0)
Chứng minh rằng f′(x) 0 ∀x ∈ R, nếu
f
(
x
)
2
3
x
9
-
x
6
+
2
x
3
-
3
x
2
+
6
x
-
1
Đọc tiếp
Chứng minh rằng f′(x) > 0 ∀x ∈ R, nếu f ( x ) = 2 3 x 9 - x 6 + 2 x 3 - 3 x 2 + 6 x - 1
Chứng minh rằng f′(x) 0 ∀x ∈ R , nếu:
f
(
x
)
3
(
sin
4
x
+
cos
4
x
)
−
2
(
sin
6
x
+
cos
6
x
)
Đọc tiếp
Chứng minh rằng f′(x) = 0 ∀x ∈ R , nếu: f ( x ) = 3 ( sin 4 x + cos 4 x ) − 2 ( sin 6 x + cos 6 x )
Chứng minh các biểu thức đã cho không phụ thuộc vào x.
f(x) = 1 ⇒ f′(x) = 0
Đúng 0
Bình luận (0)
Chứng minh rằng: Nếu x-y+z=0 thì x.y+y.z-z.x >=0
Chứng minh rằng: nếu x0 một nghiệm của đa thức P(x)=ax+b ( a khác 0) thì P(x) =a(x-x0)
chứng minh rằng nếu x-y+z=0 thì xy+yz-zx lớn hơn hoặc bằng 0
Lời giải:
Khi $x-y+z=0\Rightarrow y=x+z$. Thay vào biểu thức $xy+yz-xz$ thì:
$xy+yz-xz=x(x+z)+(x+z)z-xz=x^2+xz+z^2=x^2+\frac{xz}{2}+\frac{xz}{2}+\frac{z^2}{4}+\frac{3}{4}z^2$
$=(x+\frac{z}{2})^2+\frac{3}{4}z^2$
Dễ thấy $(x+\frac{z}{2})^2\geq 0; \frac{3}{4}z^2\geq 0$ với mọi $x,y,z$ nên $xy+yz-xz\geq 0$
Ta có đpcm.
Đúng 0
Bình luận (0)