Cho tam giác ABC. E và D lần lượt là trung điểm của các cạnh AB và AC Gọi G là giao điểm CE và BD: H và K là trung điểm BG và CG
tam giác ABC cần điều kiện j để tứ giác DEHK là hình chữ nhật hình vuông hình thoi
Bài 6: Cho tam gíac ABC, E; D lần lượt là trung điểm của các cạnh AB; AC. Gọi G là giao điểm
của CE và BD. H và K lần lượt là trung điểm của BG và CG.
a) Tứ giác DEHK là hình gì? Tại sao?
b) Tam giác ABC cần thảo mãn điều kiện gì thì tứ giác DEHK là hình chữ nhật.
c) Trong điều kiện b, hãy tính tỷ số diện tích của hình chữ nhật DEHK với diện tích tam giác ABC.

a)
ta có G là trọng tâm của tam giác ABC.
\(\hept{\begin{cases}\Rightarrow BH=GH=GD\\\Rightarrow EG=GK=KC\end{cases}}\)
hay G là trung điểm của EK và HD.
tứ giác EDKH có 2 đường chéo cắt nhau tại trung điểm mỗi đường
do đó tứ giác EDKH là hình bình hành.
b) để hình bình hành EDKH là hình chữ nhật thì EK=HD
⇒BD=EC⇒ΔABCcân
vậy để hình bình hành EDKH là hình chữ nhật thì tam giác ABC cân
c) vẽ đường cao AI vuông góc với BC.
khi đó AI cũng là đường trung tuyến.
\(\Rightarrow AG=\frac{2}{3}AI\)
ta có :\(\hept{\begin{cases}BE=AE\\AD=DC\end{cases}}\) nên ED là đường trung bình của tam giác ABC.
⇒\(\hept{\begin{cases}ED//BC\\2ED=BC\end{cases}}\)
vì ED//BC và AI⊥BC nên ED⊥AI
đồng thời EH⊥ED nên EH//AI.
ta có: \(\hept{\begin{cases}EH//AI\\BE=EA\end{cases}}\)\(\Rightarrow AH=\frac{AG}{2}\)
hay \(EH=\frac{\frac{2}{3}AI}{2}=\frac{1}{3}AI\Leftrightarrow3EH=AI\)
\(S\Delta ABC=\frac{AI.BC}{2}=\frac{3EH.2ED}{2}=3EH.ED\)=\(3S_{EDHK}\)
vậy\(\frac{S_{EDHK}}{S_{\Delta ABC}}=\frac{1}{3}\)
CHÚC BẠN HỌC TỐT
Cho tam giác ABC có đường trung tuyến BD và CE cắt nhau tại G .K,H lần lượt là trung điểm của CG và BG
A/ chứng minh tứ giác DEHK là hình bình hành
b/ điều kiện của tam giác ABC để DEHK là hình chữ nhật
A) ta có : ED là đường trung bình của tam giác ABC vậy ED song song với BC và ED=1/2BC*
HK là đường trung bình của tam giác BGC vậy HK song song với BC và HK=1/2BC**
Từ *và ** suy ra : ED=HK=1/2BC; ED song song với HK
vậy suy ra tứ giác EDHK là HBH
B) Nếu cần điều kiện từ tam giác ABC để tứ giác EDHK là HCN thì tam giác ABC cân tại A
Vì khi tam giác ABC cân tại A thì ta sẽ có : EB=DC
xét tam giác EBC và tam giác DCB có :
EB=DC ( theo CM trên )
BC cạnh chung
góc EBC = góc DCB ( vì ta đưa ra giả thiết tam giác ABC cân tại A)
vậy tam giác EBC= tam giác DCB
suy ra : EC=DB
mà ta lại có : EK=1/2EC
DH=1/2DB
vậy EK=DB: mà theo phần a ta lại có tứ giác DEHK là HBH
vậy tứ giác DEHK là HCN
cho tam giác ABC có 3 góc nhọn, các đường trung tuyến BD,CE cắt nhau tại G. gọi K và H lần lượt là trung điểm của GA và GC
a) CMR tứ giác DEHK là hình bình hành
b)tam giác ADC cần có thêm điều kiện gì để tứ giác DEHK là hình chữ nhật
a) Xét \(\Delta ABC\)có:
\(AE=BE\)(giả thiết)
\(AD=CD\)(giả thiết)
\(\Rightarrow DE\)là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DE//BC\)(tính chất) (1)
Và \(2DE=BC\)(tính chất) (2)
Xét \(\Delta GBC\)có:
\(GH=BH\)(giả thiết)
\(GK=CK\)(giả thiết)
\(\Rightarrow HK\)là đường trung bình của \(\Delta ABC\)
\(\Rightarrow HK//BC\)(tính chất) (3)
Và \(2HK=BC\)(tính chất) (4)
Từ (1) và (3)
\(\Rightarrow ED//HK\)(5)
Từ (2) và (4)
\(\Rightarrow2DE=2KH\Rightarrow DE=KH\)(6)
Xét tứ giác DEHK có: (5) và (6).
\(\Rightarrow DEHK\)là hình bình hành (điều phải chứng minh)
b) Xét \(\Delta ABC\)có 2 trung tuyến BD và CE cắt nhau tại G (giả thiết)
\(\Rightarrow\)G là trọng tâm của \(\Delta ABC\)
Do đó AG đi qua trung điểm của BC.
Mà M là trung điểm của BC (giả thiết)
Suy ra AG đi qua M.
\(\Rightarrow\)3 điểm A, G, M thẳng hàng (điều phải chứng minh).
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC
a) Chứng minh rằng tứ giác DEHK là hình bình hành
b) Tam giác ABC có điều kiện gì thì tứ giác DEHK là hình chữ nhật
c) Nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì ?
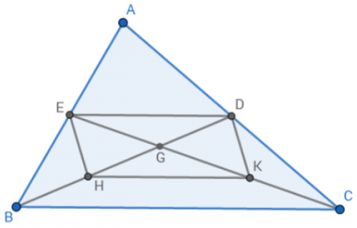
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi
Bài 1:Cho tam giác ABC, điểm I nằm giữa B và C
Qua I vẽ đường thẳng song song vs AB, cắt AC ở H
Qua I vẽ đường thẳng song song vs AC, cắt AB ở K
a) Tứ giác AHIK là hình gì?
b) Điểm I ở vị trí nào trên cạnh BC thì tứ giác AHIK là hình thoi?
c) Tam giác ABC có điều kiện gì thì tứ giác AHIK là hcn?
Bài 2: Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng vs d qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng vs D qua AC, F là giao điểm của DN và AC
a) Tứ giác AEDF là hình gì? Vì sao?
b) Các tứ giác ADBM, ADCN là hình gì? Vì sao?
c) CMR: M đối xứng vs N qua A
d) Tam giác vuông ABC có điều kiện gì thì tứ giác ADEF ,là hình vuông
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. gọi D là điểm đối xứng vs H qua AB, gọi E là điểm đx vs H qua Ac
a) CM D đx vs E qua A
b) Tam giác DHE là tam giác gì? Vì sao?
c) Tứ giác BNEC là hình gì? Vì sao
d) CMR BC= BD+CE
Bài 3: Cho tứ giác ABCD. Gọi E,F,G,H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm đk của tứ giác ABCD để EFGH là:
a) Hình chứ nhật ; b) Hình thoi ; c) hình vuông
Bài 4: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm GB, K là trung điểm của GC.
a) CMR: Tứ giác DEHK là hbh
b) Tam giác ABC có đk j thì tứ giác DEHK là hcn
c) Nếu các đường trung tuyến BN và CE vuông góc vs nhau thì tứ giác DEHK là hình j?
cho tam giác ABC có 3 góc nhọn, trung tuyến BD và CE cắt nhau tại G. Gọi H và K là trung điểm GB và GC.
a) chứng minh tứ giác DEHK là hình bình hành.
b) tam giác ABC cần thêm điều kiện gì để tứ giác DEHK là hình chữ nhật?Vì sao
c) giả sử BD vuông góc với CE thì tứ giác DEHK là hình gì?
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm GB, K là trung điểm GC
a) chứng minh tứ giác DEHK là hbh
b) tam giác ABC có điều kiện gì thì DEHK là hình chữ nhật
c) nếu đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì