Cho hàm số lẻ của x:y = g(x) = {x}
a)Tính g(-3,6);g(0,3);g(8)
Cho hàm số phần nguyên : f(x) = [x] và hàm số phần lẻ : g(x) = {x}.
a, Tính giá trị của hàm số trên tại -4,6; 1,2; 17.
b, Tìm x để f(x) = 0
c, Tìm x để g(x) = 0.
Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).
Xét các mệnh đề:
i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵn
ii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵn
iii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻ
Số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. Tất cả đều sai
Cho hai hàm số f(x)= 1 x - 3 + 3 sin 2 x và g(x)= sin 1 - x .
Kết luận nào sau đây đúng về tính chẵn lẻ của hai hàm số này?
A. Hai hàm số f(x); g(x) là hai hàm số lẻ.
B. Hàm số f(x) là hàm số chẵn; hàm số g(x) là hàm số lẻ.
C. Cả hai hàm số f(x); g(x) đều là hàm số không chẵn không lẻ.
D. Hàm số f(x) là hàm số lẻ; hàm số g(x) là hàm số không chẵn không lẻ.
Cho hai hàm số f(x) = 1 x - 3 + 3 sin 2 x và g(x) = sin 1 - x . Kết luận nào sau đây đúng về tính chẵn lẻ của hai hàm số này?
A. Hai hàm số là hai hàm số lẻ.
B. Hàm số f(x) là hàm số chẵn; hàm số g(x) là hàm số lẻ.
C. Hàm số f(x) là hàm số lẻ; hàm số g(x) là hàm số không chẵn không lẻ.
D. Cả hai hàm số đều là hàm số không chẵn không lẻ.
Đáp án D
a, Xét hàm số f ( x ) = 1 x - 3 + 3 sin 2 x có tập xác định là D = R\{3}.
Ta có x = -3 ∈ D nhưng -x = 3 ∉ D nên D không có tính đối xứng. Do đó ta có kết luận hàm số f(x) không chẵn không lẻ.
b, Xét hàm số g ( x ) = sin 1 - x có tập xác định là D2 = [1; + ∞). Dễ thấy D2 không phải là tập đối xứng nên ta kết luận hàm số g(x) không chẵn không lẻ.
Cho hai hàm số f ( x ) = 1 x - 3 + 3 sin 2 x và g ( x ) = sin 1 - x . Kết luận nào sau đây đúng về tính chẵn lẻ của hai hàm số này?
A. Hai hàm số f(x); g(x) là hai hàm số lẻ.
B. Hàm số f(x) là hàm số chẵn; hàm số g(x) là hàm số lẻ
C. Cả hai hàm số f(x), g(x) đều là hàm số không chẵn không lẻ.
D. Hàm số f(x) là hàm số lẻ, hàm số g(x) là hàm sỗ không chẵn không lẻ.
Cho hai hàm số f ( x ) = 1 x - 3 + 3 sin 2 x và g ( x ) = sin 1 - x . Kết luận nào sau đây đúng về tính chẵn lẻ của hai hàm số này?
A. Hai hàm số f(x); g(x) là hai hàm số lẻ.
B. Hàm số f(x) là hàm số chẵn; hàm số g(x) là hàm số lẻ.
C. Cả hai hàm số f(x); g(x) đều là hàm số không chẵn không lẻ.
D. Hàm số f(x) là hàm số lẻ; hàm số g(x) là hàm số không chẵn không lẻ.
Xét tính chẵn, lẻ của hai hàm số: f ( x ) = x + 2 - x - 2 , g ( x ) = - x
A. f(x) là hàm số chẵn, g(x)là hàm số chẵn.
B. f(x) là hàm số lẻ,g(x) là hàm số chẵn.
C. f(x) là hàm số lẻ, g(x) là hàm số lẻ.
D. f(x) là hàm số chẵn, g(x) là hàm số lẻ.
Đáp án B
+ Hàm số f(x) và g(x) đều có tập xác định là D= R.
+ Xét hàm số y=f(x) : Với mọi ![]() và
và
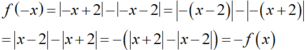
Nên y= f(x) là hàm số lẻ.
+ Xét hàm số y = g(x) :
Với mọi ![]() nên y = g(x) là hàm số chẵn.
nên y = g(x) là hàm số chẵn.
Chọn B.
Xét tính chẵn, lẻ của hai hàm số f(x) = |x + 2| − |x − 2|, g(x) = −|x|
A. f(x) là hàm số chẵn, g(x) là hàm số chẵn
B. f(x)là hàm số lẻ, g(x) là hàm số chẵn
C. f(x)là hàm số lẻ, g(x) là hàm số lẻ.
D. f(x)là hàm số chẵn, g(x) là hàm số lẻ
Xét tính chẵn, lẻ của hàm số \(g\left( x \right) = \frac{1}{x}\).
Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ 0 \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(g\left( { - x} \right) = \frac{1}{{ - x}} = - \frac{1}{x} = - g\left( x \right),\;\forall x\; \in \;D\).
Vậy \(g\left( x \right) = \frac{1}{x}\) là hàm số lẻ