Cho hàm số y=2x - 2 và y= -x + 3
a) Nêu tính chất mỗi hàm số
b) Vẽ đồ thị trên cùng 1 mặt phẳng
c) Tìm toạ độ giao điểm của 2 đường thẳng đó
d) Tính chu vi và diện tích của tam giác tạo bởi giao điểm 2 đường thẳng với trục Ox
Những câu hỏi liên quan
Cho 2 hàm số : y 2x+4 có đồ thị là đường thẳng (d) và y -x+1 có đồ thị là đường thẳng ( d1)a, vẽ đồ thị của hai hàm số trên cùng mặt phẳng tọa độ Oxyb. gọi giao của đường thẳng (d) và (d1) với nhau là C ; giao của các đường thẳng (d) với (d1) với trục Ox là A và B . Tìm tọa độ các điểm A , B , C bằng phép tính . Tính diện tích của tam giác ABC .c, Tính góc tạo bởi đường thẳng y 2x+4 với trục Ox ( làm tròn đến độ )
Đọc tiếp
Cho 2 hàm số : y = 2x+4 có đồ thị là đường thẳng (d) và y = -x+1 có đồ thị là đường thẳng ( d1)
a, vẽ đồ thị của hai hàm số trên cùng mặt phẳng tọa độ Oxy
b. gọi giao của đường thẳng (d) và (d1) với nhau là C ; giao của các đường thẳng (d) với (d1) với trục Ox là A và B . Tìm tọa độ các điểm A , B , C bằng phép tính . Tính diện tích của tam giác ABC .
c, Tính góc tạo bởi đường thẳng y = 2x+4 với trục Ox ( làm tròn đến độ )
jdhjdhshfsjsxhxhxx udjdghxhjxhg
sao dạo này toàn người cho toán lớp 9 nhỉ khó qué
cho hai hàm số bậc nhất y=-2x+5 (d) và y=0,5x (d')
a) vẽ đồ thị (d) và (d') của 2 hàm số đã cho trên cùng 1 hệ tọa độ Oxy
b) tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính )
c) Tính góc α tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ)
d) Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA
Cho hàm số y : x+2 (d) a) Vẽ đồ thị hàm số trên mặt phẳng tọa độ Oxy
b) Gọi A,B là giao điểm của đường thẳng với 2 trục tọa độ. Xác định tọa độ của A,B và tính diện tích tam giác ABC
c)Tính góc tạo bởi đường thẳng với trục
Xem chi tiết
Cho hàm số y : x+2 (d)a) Vẽ đồ thị hàm số trên mặt phẳng tọa độ Oxyb) Gọi A,B là giao điểm của đường thẳng với 2 trục tọa độ. Xác định tọa độ của A,B và tính diện tích tam giác ABCc)Tính góc tạo bởi đường thẳng với trục
Xem chi tiết
a:
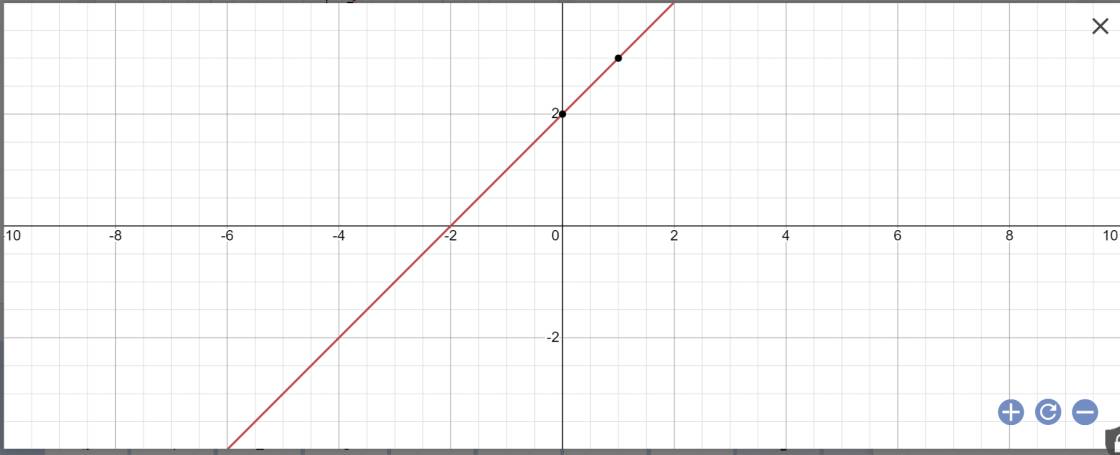
b:
Sửa đề: Tính diện tích tam giác ABO
tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\x+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Vậy: A(-2;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+2=2\end{matrix}\right.\)
Vậy: B(0;2)
O(0;0) A(-2;0); B(0;2)
\(OA=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{4}=2\)
\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=\sqrt{4}=2\)
\(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
Vì \(OA^2+OB^2=AB^2\)
nên ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)
c: Sửa đề: Tính góc tạo bởi đường thẳng với trục ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
Đúng 0
Bình luận (0)
cho hai hàm số y= 2x-4 (d) và y = -x+4 (d')
a) vẽ đồ thị hai hàm số trên cùng mặt phẳng tọa độ ?
b) Gọi giao điểm của đường thẳng (d) và(d') với trục Oy là N và M , giao điểm của hai đường thẳng là Q.
Xác định tỏa độ điểm Q và tính diện tích tam giác MNQ ? tính các góc của tam giác MNQ?
a:
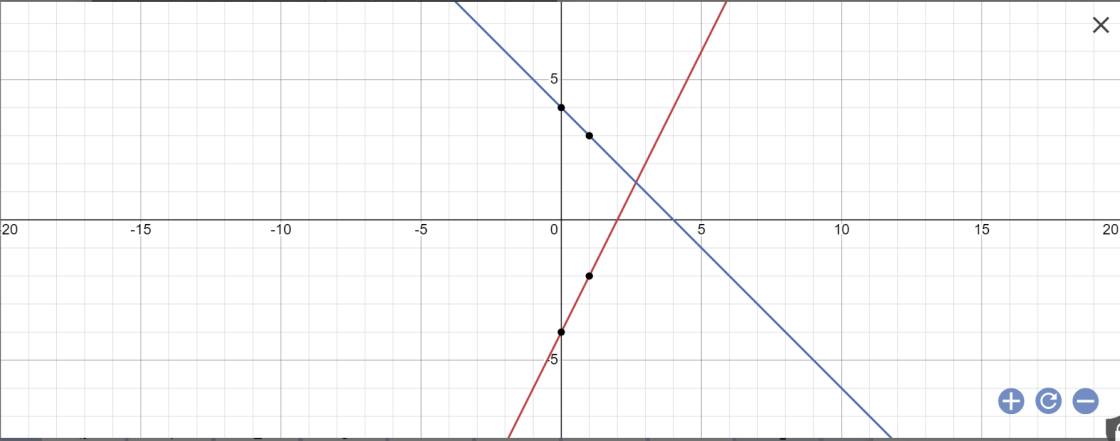
b: Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}2x-4=-x+4\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=8\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{8}{3}\\y=-\dfrac{8}{3}+4=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(Q\left(\dfrac{8}{3};\dfrac{4}{3}\right)\)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: M(0;-4)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
vậy: N(0;4)
Q(8/3;4/3); M(0;-4); N(0;4)
\(QM=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
Xét ΔMNQ có
\(cosMQN=\dfrac{QM^2+QN^2-MN^2}{2\cdot QM\cdot QN}=\dfrac{-1}{\sqrt{10}}\)
=>\(\widehat{MQN}\simeq108^026'\)
\(sinMQN=\sqrt{1-cos^2MQN}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác MQN là:
\(S_{MQN}=\dfrac{1}{2}\cdot QM\cdot QN\cdot sinMQN\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{10}}\cdot\dfrac{8\sqrt{5}}{3}\cdot\dfrac{8\sqrt{2}}{3}=\dfrac{32}{3}\)
Đúng 1
Bình luận (0)
a) vẽ đồ thị hàm số sau trên cùng mặt phẳng toạ độ Oxy
(d): y = x - 2
(d’): y = - 2x + 1
b) tìm toạ độ giao điểm E của 2 đường thẳng (d) và (d')
c) hãy tìm m để đồ thị hàm số y= (m-2)x+m và 2 đường thẳng (d),(d') đồng qui
cho hai hàm số bậc nhất y=-2x+5(d) và y=0.5x(d') .
a, vẽ đồ thị (d) và(d') của hai hàm số đã cho trên cùng một hệ trục tọa độ xOy
b, tìm tọa độ giao điểm M là giao điểm của hai đô thị vừa vẽ{bằng phép tính}
c, tính góc a tạo bởi đường thẳng (d) với trục hoành Ox
d. gọi giao điểm của (d) với trục Oy là A ,tính chu vi và diện tích tam giác MOA
Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y=x^2 và đường thẳng (d): y=-x+2
a, Vẽ đồ thị của 2 hàm số trên cùng 1 hệ trục tọa độ
b, Tìm tọa độ giao điểm của (P) và (d)
c, Gọi A,B là 2 giao điểm của (P) và (d). Tính diện tích tam giác OAB
a: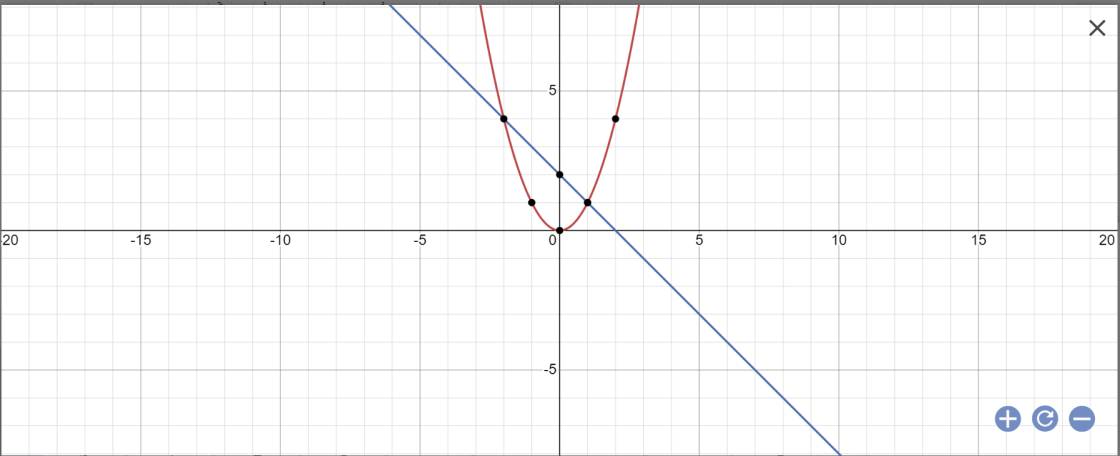 
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
Đúng 0
Bình luận (0)
Cho 2 hàm số \(y=\frac{2}{3}x+2\) và \(y=-2x-2\)
a) Vẽ đồ thị của 2 hàm số trên cùng một mặt phẳng toạ độ
b) Tìm toạ độ giao điểm M của 2 đường thẳng bằng phép tính
c) Gọi giao điểm của 2 đường thẳng với trục Ox lần lượt là N, P. Tính các góc của tam giác MNP
| 7777777777777777777777777777777lpll. | |
Cho hàm số y = 2x có đồ thị là (D1) và hàm số y = 2 /1 x – 3 có đồ thị là (D2). a) Vẽ (D1), (D2) trên cùng một mặt phẳng toạ độ. b) Tìm toạ độ giao điểm của (D1) và (D2) bằng phép tính
Bạn ghi rõ đề ở chỗ (d2) là pt nào đi bạn
Đúng 0
Bình luận (0)