Tìm GTNN của A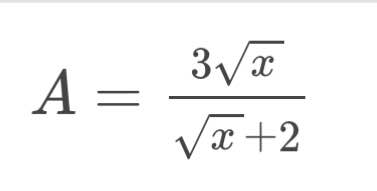

Những câu hỏi liên quan
a,Tìm GTNN của A = | x - 3 | + ( 50 )
b,Tìm GTNN của B = 2014 - | x+8 |
c, Tìm GTNN của C = | x-100 | + | y +2014 | - 2015
a, Ta có: A =| x - 3 | + 50 \(\ge50\)
\(\Leftrightarrow MinA=50.\)Dấu '=' xảy ra khi và chỉ khi x-3 = 0 \(\Leftrightarrow\) x=3
b, Ta có: B =2014 - | x + 8 | \(\ge2014\)
\(\Leftrightarrow MaxB=2014.\)Dấu '=' xảy ra khi và chỉ khi x+8=0\(\Leftrightarrow\) x=-8
CÂU NÀY PHẢI TÌM GTLN NHA BN! GTNN KO CÓ ĐÂU!
c, Ta có: C = | x-100 | + | y +2014 | - 2015 \(\ge-2015\)
\(\Leftrightarrow MinC=-2015.\)Dấu '=' xảy ra khi và chỉ khi \(\hept{\begin{cases}x-100=0\\y+2014=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=100\\y=-2014\end{cases}}\)
Đúng 0
Bình luận (0)
Cho x + y + z = 3
a, Tìm GTNN của A = x2 + y2 + z2
b, Tìm GTNN của B = xy + yz + zx
c, Tìm GTNN của C = A + B
a, ap dung bunhiacopxki
(1+1+1)A\(\ge\)(x+y+z)2=9
A\(\ge\)3
Dau bang xay ra khi x=y=z=1
b, co Bmax ko co Bmin
Đúng 0
Bình luận (0)
a,Tìm GTNN của A = | x - 3 | + ( 50 ) b,Tìm GTNN của B = 2014 - | x+8 | c, Tìm GTNN của C = | x-100 | + | y +2014 | - 2015
MỌI NGƯỜI GIÚP MK NHA MK CẦN GẤP HẬU TẠ SAU
a, Vì |x-3| \(\ge\)0
=>A=|x-3|+50\(\ge\)50
Dấu "=" xảy ra khi x=3
Vậy GTNN của A = 50 khi x=3
b, Vì |x+8| \(\ge0\)
=>B=2014-|x+8|\(\le2014\)
Dấu "=" xảy ra khi x=-8
Vậy GTLN của B = 2014 khi x=-8
c, Vì \(\hept{\begin{cases}\left|x-100\right|\ge0\\\left|y+2014\right|\ge0\end{cases}}\)
\(\Rightarrow\left|x-100\right|+\left|y+2014\right|\ge0\)
\(\Rightarrow C=\left|x-100\right|+\left|y+2014\right|-2015\ge-2015\)
Dấu "=" xảy ra khi x=100,y=-2014
Vậy GTNN của C=-2015 khi x=100,y=-2014
Đúng 0
Bình luận (0)
Tìm GTNN của A và tìm x khi A đạt GTNN biết A =|x-2018|+|x-2020|+|x-2022|
Lời giải:
Sử dụng BĐT sau:
Cho $a,b$ thực. Khi đó $|a|+|b|\geq |a+b|$. Dấu "=" xảy ra khi $ab\geq 0$. Áp dụng vào bài toán:
$|x-2018|+|x-2022|=|x-2018|+|2022-x|\geq |x-2018+2022-x|=4$
$|x-2020|\geq 0$ (theo tính chất trị tuyệt đối)
$\Rightarrow A\geq 4+0=4$
Vậy GTNN của $A$ là $4$. Giá trị này đạt được khi $(x-2018)(2022-x)\geq 0$ và $x-2020=0$
Hay khi $x=2020$
Đúng 0
Bình luận (1)
@Vũ Văn Tuần:
Để biết vì sao $|a|+|b|\geq |a+b|$ đạt dấu "=" khi $ab\geq 0$ thì bạn đi chứng minh BĐT này thôi.
Xét các TH sau:
TH1: Ít nhất 1 trong 2 số bằng 0. Không mất tính tổng quát giả sử $a=0$. Khi đó: $|a|+|b|=|b|=|b+0|=|a+b|$
TH2: $a,b$ đều khác 0. Xét các TH nhỏ hơn:
TH2.1: $a,b$ cùng dương kéo theo $a+b$ dương. Khi đó:
$|a|=a; |b|=b; |a+b|=a+b$
$\Rightarrow |a|+|b|=|a+b|$
TH2.2: $a,b$ cùng âm thì kéo theo $a+b<0$ Khi đó:
$|a|=-a; |b|=-b; |a+b|=-(a+b)$
$\Rightarrow |a|+|b|=-a+(-b)=-(a+b)=|a+b|$
TH2.3: $a,b$ khác dấu. Không mất tính tổng quát giả sử $a$ dương $b$ âm.
$\Rightarrow |a|=a; |b|=-b$
Nếu $a+b\geq 0$ thì $|a+b|=a+b$
$\Rightarrow |a|+|b|-|a+b|=a+(-b)-(a+b)=-2b>0$ do $b<0$
$\Rightarrow |a|+|b|> |a+b|$
Nếu $a+b<0$ thì $|a+b|=-(a+b)$
$\Rightarrow |a|+|b|-|a+b|=a+(-b)--(a+b)=a+(-b)+a+b=2a> 0$ do $a>0$
$\Rightarrow |a|+|b|> |a+b|$
Từ các TH đã xét ta suy ra $|a|+|b|\geq |a+b|$
Dấu "=" xảy ra khi $a,b$ cùng dương, $a,b$ cùng âm hoặc ít nhất 1 trong 2 số $a,b$ bằng $0$
Tức là $ab\geq 0$
Đúng 0
Bình luận (0)
Tìm GTLN,GTNN A= 4x-9-x*2 tìm GTLN của AB= 25x*2+3y*2+10x+11 tìm GTNN củaBC=(x-3)*2+(x-11)*2 tìm GTNN của CD= (x+1) (x-2) (x-3) (x-6) tìm GTNN củaDGiúp mình nhé
Xem chi tiết
a) Tìm GTNN của biểu thức A = x2 - 2x +5
b) Tìm GTNN của biểu thức B = 2x2 - 6x
c) Tìm GTNN của biểu thức C = 4x - x2 = 3
a) x2 - 2x + 5 = (x - 1)2 + 4 >= 4
Min là 4 khi x = 1
Đúng 0
Bình luận (0)
tìm GTNN, GTLN của biểu thức
a, A= | 3x+8,4 |-14,2 (tìm GTNN)
b, B= -| 10,2-3x |-14 (tìm GTLN)
c, C= | x-2002 |+| x-2001 | (tìm GTNN)
1. tìm GTNN của A= x(x+2)(x+4)(x+6)+8
2. tìm GTLN của B=5+(1-x)(x+2)(x+3)(x+6)3
3.tìm GTNN của C=(x+3)4 + (x-7)4
4. Cho x>0. Tìm GTNN của P=\(\dfrac{4x^2+1}{2x}\)
1.
$x(x+2)(x+4)(x+6)+8$
$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$
$=a(a+8)+8$ (đặt $x^2+6x=a$)
$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$
Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$
Đúng 4
Bình luận (0)
2.
$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$
$=5-(x^2+5x-6)(x^2+5x+6)$
$=5-[(x^2+5x)^2-6^2]$
$=41-(x^2+5x)^2\leq 41$
Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$
Đúng 4
Bình luận (0)
3.
Đặt $x+3=a; 7-x=b$ thì $a+b=10$
$C=a^4+b^4$
Áp dụng BĐT Bunhiacopxky:
$(a^4+b^4)(1+1)\geq (a^2+b^2)^2$
$\Rightarrow C\geq \frac{(a^2+b^2)^2}{2}$
$(a^2+b^2)(1+1)\geq (a+b)^2=100$
$\Rightarrow a^2+b^2\geq 50$
$\Rightarrow C\geq \frac{50^2}{2}=1250$
Vậy $C_{\min}=1250$
Giá trị này đạt tại $a=b=5\Leftrightarrow x=2$
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
a) tìm gtnn của A = x/3+3/x-2
b) tìm gtnn của B= x^2-4xy+5y^2+2x-10y+17
Tìm Gtnn của a=(x^2+x+1)
Tìm gtnn của =(x+2)^2+(x-3)^2
x^2+x+1/4+3/4
=(x+1/2)^2+3/4
=> A min=3/4
Câu kia tương tự .......
Đúng 0
Bình luận (0)
\(A=x^2+x+1=x^2+2x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x+\frac{1}{2}\right)^2\ge0,x\in R\)
nên \(\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4},x\in R\)
Vậy \(Min_A=\frac{3}{4}\)khi \(x+\frac{1}{2}=0\Rightarrow x=-\frac{1}{2}\)
\(B=\left(x+2\right)^2+\left(x-3\right)^2=x^2+2x+1+x^2-6x+9=2x^2-4x+10=2\left(x^2-2x+5\right)\)
\(B=2\left(x^2-2x+1+4\right)=2\left(x-1\right)^2+4\)
Vì \(2\left(x-1\right)^2\ge0,x\in R\)
nên \(2\left(x-1\right)^2+4\ge4,x\in R\)
Vậy \(Min_B=4\)khi \(x-1=0\Rightarrow x=1\)
Đúng 0
Bình luận (0)


















