Chứng minh công thức tính khoảng cách giữa hai điểm A(xA;yA) và B(xB;yB) là d=\(\sqrt{\left(xA-xB\right)^2+\left(yA-yB\right)^2}\)

Những câu hỏi liên quan
Câu hỏi: Sử dụng công thức tính khoảng cách hai điểm trong mặt phẳng tọa độ để chứng minh bất đẳng thức Ptôlêmê
Công thức tính lực hấp dẫn giữa hai chất điểm có khối lượng
m
1
;
m
2
đặt cách nhau một khoảng r là: A.
F
h
d
G
m
1
m
2
r
B. ...
Đọc tiếp
Công thức tính lực hấp dẫn giữa hai chất điểm có khối lượng m 1 ; m 2 đặt cách nhau một khoảng r là:
A. F h d = G m 1 m 2 r
B. F h d = G m 1 + m 2 r 2
C. F h d = G r 2 m 1 m 2
D. F h d = G m 1 m 2 r 2
Trong hiện tượng giao thoa với khe Y-âng, khoảng cách giữa hai nguồn là a, khoảng cách từ hai nguồn đến màn là D, x là toạ độ của một điểm trên màn so với vân sáng trung tâm. Công thức tính hiệu đường đi là: A.
d
2
-
d
1
ax
D
B.
d
2
-
d
1...
Đọc tiếp
Trong hiện tượng giao thoa với khe Y-âng, khoảng cách giữa hai nguồn là a, khoảng cách từ hai nguồn đến màn là D, x là toạ độ của một điểm trên màn so với vân sáng trung tâm. Công thức tính hiệu đường đi là:
A. d 2 - d 1 = ax D
B. d 2 - d 1 = 2 ax D
C. d 2 - d 1 = ax 2 D
D. d 2 - d 1 = aD x
Trong hiện tượng giao thoa với khe Y-âng, khoảng cách giữa hai nguồn là a, khoảng cách từ hai nguồn đến màn là D, x là tọa độ một chất điểm trên màn so với vân trung tâm. Công thức tính hiệu đường đi là A.
d
2
-
d
1
aD/x B.
d
2
-
d
1
2ax/D C.
d
2
-...
Đọc tiếp
Trong hiện tượng giao thoa với khe Y-âng, khoảng cách giữa hai nguồn là a, khoảng cách từ hai nguồn đến màn là D, x là tọa độ một chất điểm trên màn so với vân trung tâm. Công thức tính hiệu đường đi là
A. d 2 - d 1 =aD/x
B. d 2 - d 1 =2ax/D
C. d 2 - d 1 =ax/2D
D. d 2 - d 1 =ax/D
Chọn D
Phương pháp:
Sử dụng lí thuyết về giao thoa hai khe Y- âng
Cách giải:
Hiệu đường đi: d2 - d1 = ax/D
Đúng 0
Bình luận (0)
Độ lớn lực tương tác giữa hai điện tích điểm
q
1
và
q
2
đặt cách nhau một khoảng r trong chân không được tính theo công thức A.
F
k
q
1
q
2...
Đọc tiếp
Độ lớn lực tương tác giữa hai điện tích điểm q 1 và q 2 đặt cách nhau một khoảng r trong chân không được tính theo công thức
A. F = k q 1 q 2 r 2
B. F = k q 1 q 2 2 r 2
C. F = k q 1 q 2 2 r
D. F = k q 1 q 2 r
Người ta chứng minh được rằng: Khoảng cách giữa hai điểm a,b trên trục số ( a,b ∈ Z) bằng |a-b| hay |b-a|. Hãy tìm khoảng cách giữa các điểm a và b trên trục số khi: a = -3 , b = 5
Khoảng cách giữa hai điểm a và b trên trục số bằng:
| -3 -5 | = | -3 + (-5)| = |-8| = 8
Đúng 0
Bình luận (0)
Người ta chứng minh được rằng: Khoảng cách giữa hai điểm a,b trên trục số ( a,b ∈ Z) bằng |a-b| hay |b-a|. Hãy tìm khoảng cách giữa các điểm a và b trên trục số khi: a = 15, b = 37
Khoảng cách giữa hai điểm a và b trên trục số là:
|15 – 37| = |15 + (-37)| = |-22| = 22
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A'B'C'D'
a) Chứng minh rằng B'D vuông góc với mặt phẳng (BA'C')
b) Tính khoảng cách giữa hai mặt phẳng (BA'C') và (ACD')
c) Tính khoảng cách giữa hai đường thẳng BC' và CD'
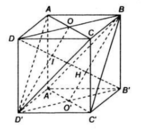

b) Xét tứ giác A’BCD’ có BC//A’D’ và BC = A’D’
=> tứ giác A’BCD’ là hình bình hành
=> BA’ // CD’ ( tính chất của hình bình hành)
Tương tự, tứ giác ABC’D’ là hình bình hành nên BC’//AD’
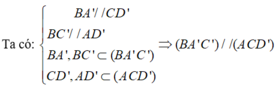
Gọi O và O’ là tâm của ABCD và A’B’C’D’.
Gọi H và I lần lượt là tâm của hai tam giác đều BA’C’ và ACD’.
* Xét ( BB’D’D) có BO’// D’O nên OI // HB
Lại có: O là trung điểm BD
=> I là trung điểm của HD: IH = ID (1)
* Xét (BB’D’D) có D’O// BO’ nên D’I // HO’
Lại có: O’ là trung điểm của B’D’ nên H là trung điểm B’I: HI = HB’ (2)
Từ (1) và (2) suy ra: 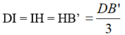
* Theo phần trên B'D ⊥ (BA'C) ⇒ IH ⊥ (BA'C)
Mà I ∈ (ACD') nên khoảng cách giữa hai mp song song (ACD’) và ( BA’C’) là độ dài đoạn IH.
Khi đó:
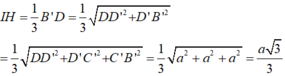
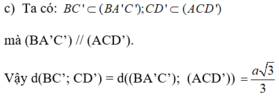
Đúng 0
Bình luận (0)
CHỨNG MINH: Nếu 2 điểm A,B nằm trên cùng một tia gốc O thì khoảng cách giữa các trung điểm M và N của hai đoạn thẳng OA và OB bằng nữa khoảng cách giữa 2 điểm A và B
giup roi nha bb








