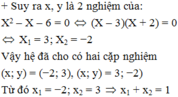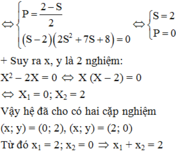chứng minh x1+x2+x3+........+xm/y1+y2+y3+.......+ym=q/p

Những câu hỏi liên quan
Cho (x1*p-y1*q) ^ 2n+(x2*p-y2*q) ^ 2n+...+(xm*p-ym*q) ^ 2n < hoặc = 0. CMR (x1+x2+...+xm)/(y1+y2+...+ym) = q/p (
Cho (x1*p-y1*q) ^ 2n+(x2*p-y2*q) ^ 2n+...+(xm*p-ym*q) ^ 2n < hoặc = 0. CMR (x1+x2+...+xm)/(y1+y2+...+ym) = q/p
Cho: \(\left(x_1p-y_1q\right)^{2n}+\left(x_2p-y_2q\right)^{2n}+\left(x_3p-y_3q\right)^{2n}+...+\left(x_mp-y_mq\right)^{2n}\le0\) với mọi m, n \(\in\)N*
Chứng minh rằng : \(\frac{x1+x2+x3+...+xm}{y1+y2+y3+...+ym}\)=\(\frac{q}{p}\)
Có vẻ như giữa (x2p - y2q)2n và (x3p - y3q)2n thiếu dấu + thì phải?
Ta có thể chứng minh như sau:
Với mọi n thuộc tập N*, ta có: k2n >= 0 với mọi k. (1)
-> (x1p - y1q)2n + ... + (xmp - ymq)2n luôn bằng 0
-> x1p - y1q = 0, x2p - y2q = 0, ... và xmp - ymq = 0 (2)
Giả sử điều cần chứng minh là đúng: (x1 + ... + xm) / (y1 + ... + ym) = q / p
-> p*(x1 + ... + xm) = q*(y1 + ... + ym)
-> x1p + ... + xmp = y1q + ... + ymq
-> (x1p - y1q) + ... (xmp - ymq) = 0 (3)
Theo (2), (3) luôn đúng -> Giả sử của ta là chính xác.
Đúng 0
Bình luận (0)
sai cmnr ko nen lam theo
Cho x,y là 2 đại lượng tỉ lệ thuận ; x1,x2,x3 là 3 giá trị khác nhau của x với x1-x2=3(x3-x2+672)
y1,y2,y3 là 3 giá trị tương ứng của y thỏa y2+y3=y1+5(y2-403) / 3
Viết công thức liên hệ x và y.
Biết hệ phương trình
x
3
+
y
3
19
x
+
y
8
+...
Đọc tiếp
Biết hệ phương trình x 3 + y 3 = 19 x + y 8 + x y = 2 có hai nghiệm ( x 1 ; y 1 ) ; ( x 2 ; y 2 ) . Tổng x 1 + x 2 bằng?
A. −1
B. 2
C. 1
D. 0
Biết hệ phương trình
x
3
+
y
3
8
x
+
y
+
2
x
y...
Đọc tiếp
Biết hệ phương trình x 3 + y 3 = 8 x + y + 2 x y = 2 có hai nghiệm ( x 1 ; y 1 ) ; ( x 2 ; y 2 ) . Tổng x 1 + x 2 bằng?
A. 2
B. −2
C. 1
D. 0
Cho x,y là 2 đại lượng tỉ lệ thuận ; x1,x2,x3 là 3 giá trị khác nhau của x với x1-x2=3(x3-x2+672)
y1,y2,y3 là 3 giá trị tương ứng của y thỏa y2+y3=y1+5(y2-403) / 3
Viết công thức liên hệ x và y.
MẤY BẠN GIẢI GIÚP MIK NHANH NHÉ MIK ĐG CẦN GẤP LẮM !!!
Cho xy là hai đại lượng tỉ lệ thuận với nhau. Biết x1,x2,x3 là ba giá trị khác nhau của x thỏa mãn x1 - x2 = 3(x3-x2 + 672 ) và y1,y2,y3 là các giá trị khác nhau của x thỏa mãn 3( y2 + y3 ) = y1 + 5.(y2 - 403). Viết công thức liên hệ giữa y và x
x1-x2=3(x3-x2+672)
=>x1-x2=3x3-3x2+2016
=>x1+2x2-3x3=2016
3(y2+y3)=y1+5(y2-403)
=>3y2+3y3-y1-5y2+2015=0
=>-y1-2y2+3y3=-2015
=>y1+2y2-3y3=2015
Vì x,y tỉ lệ thuận
nên x1/y1=x2/y2=x3/y3
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_3}{y_3}=\dfrac{x_1+2x_2-3x_3}{y_1+2y_2-3y_3}=\dfrac{2016}{2015}\)
=>x=2016/2015y
=>y=2015/2016x
Đúng 0
Bình luận (0)
Cho hàm số y
1
x
x
4
-
3
x
2
+
3
2
có đồ thị là (C) và điểm A
-
27
16
;
-
15
4
. Biết có ba điểm
M
1
(
x
1...
Đọc tiếp
Cho hàm số y = 1 x x 4 - 3 x 2 + 3 2 có đồ thị là (C) và điểm A - 27 16 ; - 15 4 . Biết có ba điểm M 1 ( x 1 ; y 1 ) , M 2 ( x 2 ; y 2 ) , M 3 ( x 3 ; y 3 ) thuộc sao cho tiếp tuyến của tại mỗi điểm đó đều đi qua A. Tính S = x 1 + x 2 + x 3
A. S = 7 4
B. S = - 3
C. S = - 5 4
D. S = 5 4
Chọn C.
Gọi ![]() Khi đó phương trình tiếp tuyến
M
0
là
Khi đó phương trình tiếp tuyến
M
0
là
![]()
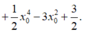
Ta có: 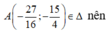
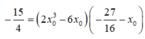
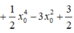
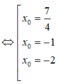
Không mất tính tổng quát của M 1 ( x 1 ; y 1 ) , M 2 ( x 2 ; y 2 ) , M 3 ( x 3 ; y 3 ) , ta có:

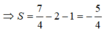
Đúng 0
Bình luận (0)