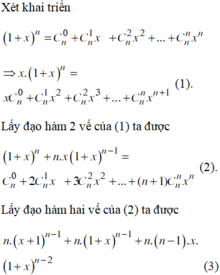Tìm số tự nhiên nn biết 1+2+...+n = 5281+2+...+n=528.

Những câu hỏi liên quan
Tìm số tự nhiên nn biết (2n^2+n+3) chia hết cho n
Tìm số tự nhiên n \ne 0n=0 nhỏ nhất sao cho khi chia nn cho 2/7và chia nn cho 3/4 ta đều được kết quả là số tự nhiên.
Tìm các số tự nhiên n sao cho các phân số sau có giá trị là số nguyên
a) C = 6 n − 1
b) D = n n − 2
Biết n là số tự nhiên thỏa mãn
1
.
2
C
n
1
+
2
.
3
C
n
2
+
.
.
.
+
n
n
+
1
C
n
n
180
.
2
n
-...
Đọc tiếp
Biết n là số tự nhiên thỏa mãn 1 . 2 C n 1 + 2 . 3 C n 2 + . . . + n n + 1 C n n = 180 . 2 n - 2 . Số hạng có hệ số lớn nhất trong khai triển 1 + x n là
A. 925 x 5
B. 924 x 6
C. 923 x 4
D. 926 x 7
Biết n là số tự nhiên thỏa mãn
1
.
2
C
n
1
+
2
.
3
C
n
2
+
.
.
.
+
n
n
+
1
C
n
n
180
.
2
n
-...
Đọc tiếp
Biết n là số tự nhiên thỏa mãn 1 . 2 C n 1 + 2 . 3 C n 2 + . . . + n n + 1 C n n = 180 . 2 n - 2 Số hạng có hệ số lớn nhất trong khai triển 1 + x n là
A. 925 x 5
B. 924 x 6
C. 923 x 4
D. 926 x 7
Tìm các cặp số tự nhiên n sao cho các phân số sau có giá trị là số nguyên: n n - 2
Để phân số n n - 2 có giá trị là số nguyên
thì n ⋮ n - 2 ⇒ n - 2 + 2 ⋮ n - 2
Mà n - 2 ⋮ n - 2 ⇒ 2 ⋮ n - 2
⇒ (n – 2) ∈ Ư(2) = {±1; ±2}
Ta có bảng sau:
| n - 2 | -1 | 1 | -2 | 2 |
| n | 1 | 3 | 0 | 4 |
Kết hợp với điều kiện n là số tự nhiên
⇒ n ∈ {0; 1; 3; 4}
Vậy n ∈ {0; 1; 3; 4}.
Đúng 0
Bình luận (0)
bài 1: tìm số tự nhiên n biết:
2 + 4 + 6 +....+ (2n) = 756
bài 2: tìm số tự nhiên n sao cho p = ( n - 2 )(n2 + n - 5) là số nguyên tố.
Bài 1:
Ta có dãy số 2, 4, 6, ..., 2n là một dãy số chẵn liên tiếp.
Ta có công thức tổng của dãy số chẵn liên tiếp là: S = (a1 + an) * n / 2
Với a1 là số đầu tiên của dãy, an là số cuối cùng của dãy, n là số phần tử của dãy.
Áp dụng công thức trên vào bài toán, ta có:
(2 + 2n) * n / 2 = 756
(2n + 2) * n = 1512
2n^2 + 2n = 1512
2n^2 + 2n - 1512 = 0
Giải phương trình trên, ta được n = 18 hoặc n = -19.
Vì n là số tự nhiên nên n = 18.
Vậy số tự nhiên n cần tìm là 18.
Bài 2:
Ta có p = (n - 2)(n^2 + n - 5)
Để p là số nguyên tố, ta có hai trường hợp:
1. n - 2 = 1 và n^2 + n - 5 = p
2. n - 2 = p và n^2 + n - 5 = 1
Xét trường hợp 1:
n - 2 = 1
=> n = 3
Thay n = 3 vào phương trình n^2 + n - 5 = p, ta có:
3^2 + 3 - 5 = p
9 + 3 - 5 = p
7 = p
Vậy n = 3 và p = 7 là một cặp số nguyên tố thỏa mãn.
Xét trường hợp 2:
n - 2 = p
=> n = p + 2
Thay n = p + 2 vào phương trình n^2 + n - 5 = 1, ta có:
(p + 2)^2 + (p + 2) - 5 = 1
p^2 + 4p + 4 + p + 2 - 5 = 1
p^2 + 5p + 1 = 1
p^2 + 5p = 0
p(p + 5) = 0
p = 0 hoặc p = -5
Vì p là số nguyên tố nên p không thể bằng 0 hoặc âm.
Vậy không có số tự nhiên n thỏa mãn trong trường hợp này.
Vậy số tự nhiên n cần tìm là 3.
Đúng 1
Bình luận (0)
Bài 1
...=((2n-2):2+1):2=756
(2(n-1):2+1)=756×2
n-1+1=1512
n=1512
Đúng 0
Bình luận (0)
Bài 2
\(\left(n-2\right)\left(n^2+n-5\right)\) là số nguyên tố khi n-2=1, suy ra n=3.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Tìm n là số tự nhiên, biết ( n+6 ) chia hết n
Bài 2: Tìm x là số tự nhiên sao cho ( 2.n - 1) . (y+ 3)=12
BAI 1
ta co n+6 chia het cho n
ma n chia het cho n
suy ra 6 chia het cho n
ma n la mot so tu nhien nen
ta co n thuoc U(6)=1,2,3,6
vay n bang 1,2,3,6
bai 2
(2n-1).(y+3)=12
suy ra 2n-1 va y+3 thuoc uoc cua 12 =1,12,3,4,6,2
neu 2n-1 =1 suy ra n=1
thi y+3=12 suy ra y=9
neu 2n-1=12 suy ra n=11/2(ko thoa man )
neu 2n-1=3 suy ra n=2
thi y+3=4 suy ra y=1
neu 2n-1=4 ruy ra n=5/2( ko thoa man )
neu 2n-1=6 suy ra n=7/2( ko thoa man )
neu 2n-1=2 suy ra n=3/2 ( ko thoa man )
vay cac cap so n :y can tim la (2;1),(1;9)
Đúng 0
Bình luận (0)
Tìm số tự nhiên y lớn hơn 1 biết tồn tại số tự nhiên n để:
y^2 = 1!+ 2! + 3! +.... + n!