cho tam giác ABC có ba góc nhọn.Gọi O là trung điểm của BC.Gọi D là điểm đối xứng của A qua BC;E là điểm đối xứng của A qua O.Chứng minh ràng BCED là hình thang cân

Những câu hỏi liên quan
Cho tam giác ABC có ba góc nhọn.Gọi O là trung điểm của BC.Gọi D là điểm đối xứng của A qua BC;E là điểm đối xứng của A qua O.Chứng minh rằng BCED là hình thang cân
a) Em hãy chứng tỏ phát biểu sau đây là sai:
"Nếu một hình thang có hai cạnh bên bằng nhau thì đó là hình thang cân"
b) Cho tam giác ABC có ba góc nhọn.Gọi O là trung điểm của BC.Gọi D là điểm đối xứng của A qua BC;E là điểm đối xứng của A qua O.
Chứng minh rằng BCED là hình thang cân.
Cho tam giác ABC vuông tại A(AB<AC) có I là trung điểm của BC.Gọi D là điểm đối xứng của A qua I,E là điểm đối xứng của A qua BC.
a) chứng minh: tứ giác ABCD là hình chữ nhật
b) chứng minh tứ giác BEDC là hình thang cân
c) trên tia đối của tia BA, lấy điểm F sao cho BF=AB. Chứng minh ba điểm D,E,F thẳng hàng.
d) giả sử góc ABC = 60 độ. chứng minh BD,AE,FI đồng quy
Cho tam giác ABC có ba góc nhọn. Gọi O là trung điểm của BC. Gọi D là điểm đối xứng của A qua BC; E là điểm đối xứng của A qua O.
Đề yêu cầu CMR : BCED là hình thang cân ??
Ta có : A đối xứng D qua BC , gọi AD cắt BC tại H ta có AD \(\perp\) BC tại H và AH = HD
Xét tg ADE ta có ; AH = HD , AO = OE
=> OH // DE hay BC // DE .
tứ giác BCED có BC//DE => BCED là hih thang .
Xét tg OAB và tg OEC có :
OB = OC , OA = OE , góc AOB = góc COE
=> tg OAB = tg OEC => góc ABO = góc OCE (1).
Có : BH \(\perp\) AD tại trung điểm H của AD
=> BAD cân tại B => góc ABH = góc HBD (2) .
Từ (1) và (2) có : góc HBD = góc OCE
=> hih thang BCED có : góc HBD = góc OCE
=> BCED là hih thang cân .
Xem thêm tại : Câu hỏi của Quang Trần - Toán lớp 8 | Học trực tuyến ( https://h.vn/hoi-dap/question/674960.html )
Gợi ý cho bạn
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc nhọn.gọi d là trung điểm của ab.lấy e đối xứng với c qua điểm d
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn ( ) O . Gọi M là trung điểm của cạnh BC và N là điểm đối xứng của M qua O . Đường thẳng qua A vuông góc với AN cắt đường thẳng qua B vuông góc với BC tại D . Kẻ đường kính AE . Chứng minh rằng:b) CD đi qua trung điểm của đường cao AH của tam giác ABC .
Đọc tiếp
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn ( ) O . Gọi M là trung điểm của cạnh BC và N là điểm đối xứng của M qua O . Đường thẳng qua A vuông góc với AN cắt đường thẳng qua B vuông góc với BC tại D . Kẻ đường kính AE . Chứng minh rằng:
b) CD đi qua trung điểm của đường cao AH của tam giác ABC .
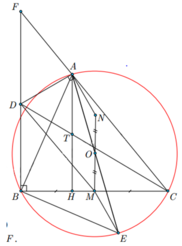
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
Đúng 0
Bình luận (0)
cho tam giác abc có 3 góc nhọn.Gọi D và O lần lượt là trung điểm của BC,AD.Qua O vẽ đường thẳng d không song song với BC.Gọi M,k,I,N lần lượt là chân các hình chiếu của B,D,A,N trên đường thẳng d.CMR:BM+CN=2AI
Có: BMNC là hình thang, KD là đường trung bình vì vậy:
\(KD=\frac{BM+NC}{2}\)
Lại có: \(\Delta AIO=\Delta DKO\) (cạnh góc vuông và góc nhọn kề) nên AI = DK.
Vậy: \(MB=CN=2DK=2AI\)
Đúng 0
Bình luận (0)
cho tam giác abc có 3 góc nhọn.Gọi D và O lần lượt là trung điểm của BC,AD.Qua O vẽ đường thẳng d không song song với BC.Gọi M,k,I,N lần lượt là chân các hình chiếu của B,D,A,N trên đường thẳng d.CMR:BM+CN=2AI
Thấy ngay BMNC là hình thang, KD là đường trung bình, vì thế nên : \(KD=\frac{BM+NC}{2}\)
Lại có: \(\Delta AIO=\Delta DKO\) (cạnh góc vuông và góc nhọn kề) nên AI = DK.
Vậy \(MB+CN=2DK=2AI.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm O nằm trong tam giác. Gọi A' là điểm đối xứng với O trung điểm D của BC, B' là điểm đối xứng với O qua trung điểm E của AC, C' là điểm đối xứng với O qua trung điểm F của AB.Chứng minh rằng tam giác ABC = tam giác A'B'C' .
Xét tam giác COA tao có FD là đường trung bình
=> FD = 1/2 A'C'
chứng minh tương tự FD = 1/2 AC => A'C' =AC
chứng minh tương tự B'C"= BC; A'B'=AB
vậy tam giác ABC =tam giác A'B'C'
Đúng 0
Bình luận (0)





















