42 - (2 x X + 32) + 12 : 2 = 6

42 - (2 x X + 32) + 6 = 6

42 - (2 x X + 32) = 0 

=> 2 x X + 32 = 42

2 x X = 10

      X = 10 : 2

      X = 5

Goodluck!!

AI NHANH MK K NHA

chọn mình nha

mình làm rùi đó

\(\Rightarrow42-2x-32+6=6\\ \Rightarrow16-2x=6\\ \Rightarrow2x=10\\ \Rightarrow x=5\)

\(\Rightarrow42-2x-32+6=6\\ \Rightarrow16-2x=6\\ \Rightarrow2x=10\\ \Rightarrow x=5\)

=>42−2x−32+6=6

=>16−2x=6

=>2x=10

=>x=5

\(42-\left(2x+32\right)+12:2=6\)

\(\Rightarrow42-\left(2x+32\right)+12=12\)

\(\Rightarrow42-\left(2x+32\right)=0\)

\(\Rightarrow2x+32=42\)

\(\Rightarrow2x=10\)

\(\Rightarrow x=5\)

42-(2x+32)+12:2=6

(2x+32)+6=42-6

(2x-32)+6=36

(2x-32)=36-6

  2x-32=30

       2x=30+32

       2x=62

         x=62:2

         x=31

Tk mk nha

42-(2x + 32) + 12 : 2=6 

42 - (2x + 32) +12 = 6:2

42- ( 2x + 32) + 12= 3

42- ( 2x + 32) = 12 - 3

42 - (2x + 32) =9

 2x +32 =42 -9 

2x +32 =33

2x = 33 -32

2x = 1

x = 2. 1

x =2

cố lên nha 

\(42-\left(2x+32\right)+12:2=6\)

\(\Rightarrow42-\left(2x+32\right)+12=12\)

\(\Rightarrow42-\left(2x+32\right)=0\)

\(\Rightarrow2x+32=42\)

\(\Rightarrow2x=10\)

\(\Rightarrow x=5\)

42-(2x+32)+12:2+6

(2x+32)+6=42-6=36

        2x+32=36-6=30

              2x=30+32=62

                x=62:2=31

tk mk nha

42-(2x+32)+12:2=6

42-(2x+32)+12=6.2

42-(2x+32)+12=12

42-(2x+32)=12-12

42-(2x+32)=0

2x+32=42-0

2x+32=42

2x=42-32

2x=10

x=10:2

x=5

42 - (2x + 32) + 12 = 6.2

42 - (2x + 32) + 12 = 12

42 - (2x + 32 )        = 12 - 12

42 - (2x + 32)        = 0

2x + 32                  = 42 - 0

2x + 32                  = 42

2x                          = 42 - 32

2x                          = 10

=> x                      = 10 : 2

=> x                       = 5

De la gi vay ban

a)

( x − 3 ) 2 + ( x + 4 ) 2 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 + 3 x − 23 = 0 ⇔ 2 x 2 + 5 x + 2 = 0

Có a = 2; b = 5; c = 2  ⇒   Δ   =   5 2   –   4 . 2 . 2   =   9   >   0

⇒ Phương trình có hai nghiệm:

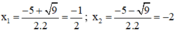
Vậy phương trình có tập nghiệm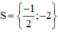 

b)

x 3 + 2 x 2 − ( x − 3 ) 2 = ( x − 1 ) x 2 − 2 ⇔ x 3 + 2 x 2 − x 2 − 6 x + 9 = x 3 − x 2 − 2 x + 2 ⇔ x 3 + 2 x 2 − x 2 + 6 x − 9 − x 3 + x 2 + 2 x − 2 = 0 ⇔ 2 x 2 + 8 x − 11 = 0

Có a = 2; b = 8; c = -11  ⇒   Δ ’   =   4 2   –   2 . ( - 11 )   =   38   >   0

⇒ Phương trình có hai nghiệm:

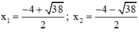
Vậy phương trình có tập nghiệm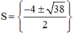 

c)

( x − 1 ) 3 + 0 , 5 x 2 = x x 2 + 1 , 5 ⇔ x 3 − 3 x 2 + 3 x − 1 + 0 , 5 x 2 = x 3 + 1 , 5 x ⇔ x 3 + 1 , 5 x − x 3 + 3 x 2 − 3 x + 1 − 0 , 5 x 2 = 0 ⇔ 2 , 5 x 2 − 1 , 5 x + 1 = 0

Có a = 2,5; b = -1,5; c = 1

⇒   Δ   =   ( - 1 , 5 ) 2   –   4 . 2 , 5 . 1   =   - 7 , 75   <   0

Vậy phương trình vô nghiệm.

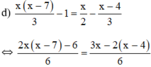
⇔ 2 x ( x − 7 ) − 6 = 3 x − 2 ( x − 4 ) ⇔ 2 x 2 − 14 x − 6 = 3 x − 2 x + 8 ⇔ 2 x 2 − 14 x − 6 − 3 x + 2 x − 8 = 0 ⇔ 2 x 2 − 15 x − 14 = 0

Có a = 2; b = -15; c = -14

⇒   Δ   =   ( - 15 ) 2   –   4 . 2 . ( - 14 )   =   337   >   0

⇒ Phương trình có hai nghiệm:

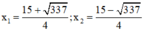
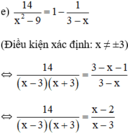
⇔ 14 = ( x - 2 ) ( x + 3 ) ⇔ 14 = x 2 - 2 x + 3 x - 6 ⇔ x 2 + x - 20 = 0

Có a = 1; b = 1; c = -20

⇒   Δ   =   1 2 –   4 . 1 . ( - 20 )   =   81   >   0

Phương trình có hai nghiệm:

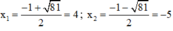
Cả hai nghiệm đều thỏa mãn điều kiện xác định.

Vậy phương trình có tập nghiệm S = {-5; 4}.

f) Điều kiện: x≠-1;x≠4

Ta có: a= 1, b = -7, c = - 8

∆   =   ( - 7 ) 2   –   4 . 1 .   ( -   8 ) =   81

=> Phương trình có hai nghiệm:

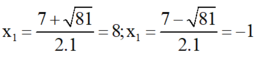
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8

42 -(2x + 32) + 12 :2 =6

42 - 2x - 32 + 6 = 6

42 - 2x - 32 = 0

42 - 2x = 32

2x = 42 - 32 = 10

x = 5

134 - 2 . {156 - 6.[54 -2.(9+6) ] } x = 86

134 - 2.{ 156 - 6.[54 - 2 . 15 ]} x = 86

134 - 2.{ 156 - 6 . 24} x = 86

134 - 2. 12 .x = 86

134 - 24x = 86

24x = 48

x = 2 

\(42-\left(2x+32\right)+12:2=6\)

\(\Rightarrow42-2x-32=0\)

\(\Rightarrow2x=10\)

\(\Rightarrow x=5\)

\(42-\left(2x+32\right)=12:2=6\)

\(42-\left(2x+32\right)+6=6\)

\(42-\left(2x+32\right)=6-6=0\)

\(2x+32=42-0=42\)

\(2x=42-32=10\)

\(x=10:2=5\)

42-(2x+32)+12:2=6

42-(2x+32)+6     =6

42-(2x+32)         =6-6

42-(2x+32)         =0

      2x+32           =42-0

      2x+32           =42

      2x                 =42-32

      2x                 =10

        x                 =10:2

        x                 =5

nhớ kick cho mình nha

a, \(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}\)

=  \(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}\)

= \(1-\frac{1}{7}=\frac{6}{7}\)