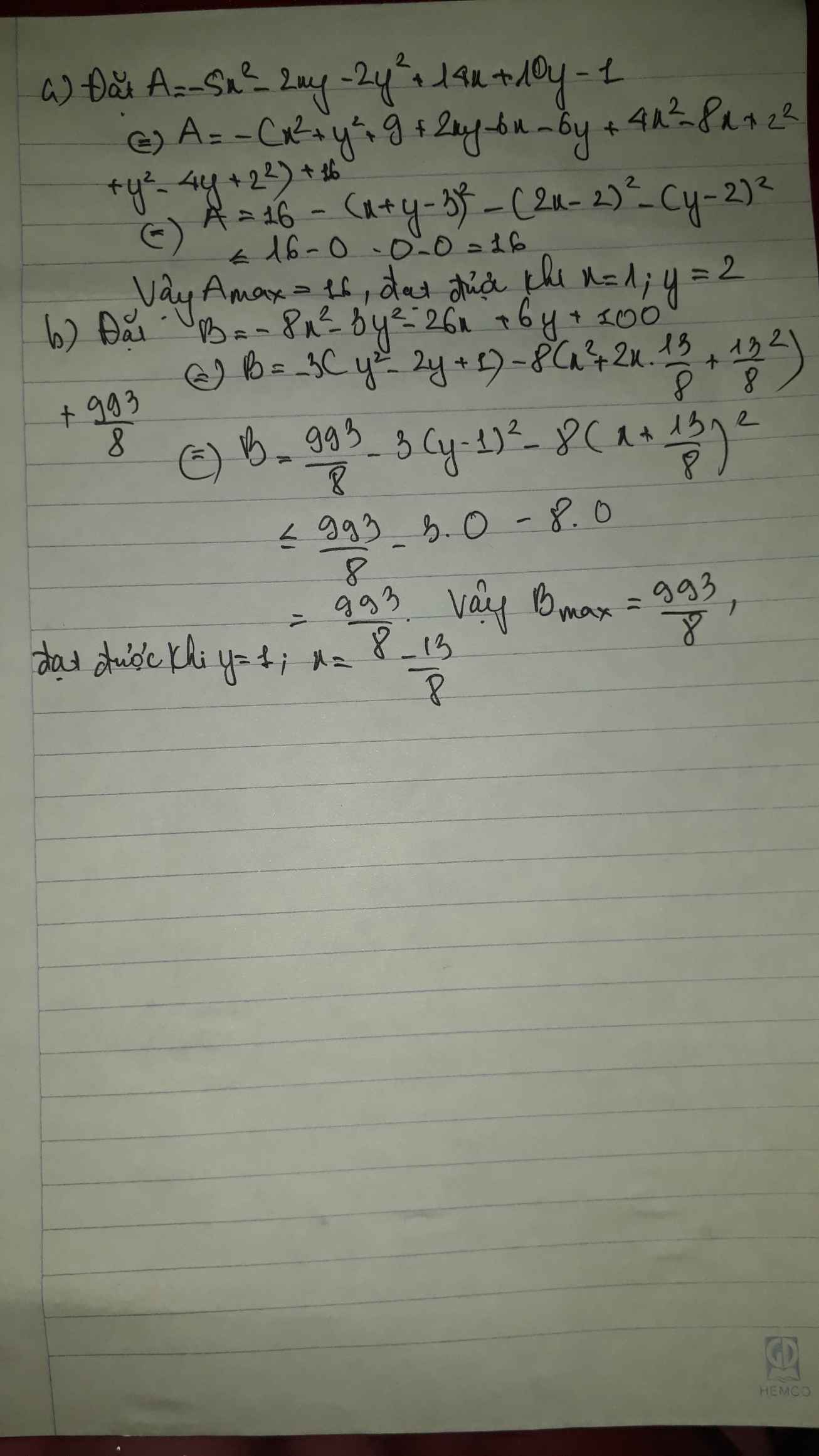\(P=-5x^2-2xy-2y^2+14x+10y-1\)

\(=-\left(4x^2-8x+4\right)-\left(y^2-4y+4\right)-\left(x^2+y^2+2xy-6x-6y+9\right)+16\)

\(=-4\left(x-1\right)^2-\left(y-2\right)^2-\left(x+y-3\right)^2+16\le16\)

Dấu \(=\)khi \(\hept{\begin{cases}x-1=0\\y-2=0\\x+y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}\).

Bài 2 :

a) \(P=x^2+y^2+xy+x+y\)

\(2P=2x^2+2y^2+2xy+2x+2y\)

\(2P=x^2+2xy+y^2+x^2+2x+1+y^2+2y+1-2\)

\(2P=\left(x+y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2-2\)

\(P=\frac{\left(x+y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2-2}{2}\)

\(P=\frac{\left(x+y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2}{2}-1\le-1\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+y=0\\x+1=0\\y+1=0\end{cases}}\)

Mình nghĩ đề phải là tìm GTLN của \(P=x^2+y^2+xy+x-y\)hoặc đổi dấu x và y thì dấu "=" mới xảy ra đc

@ Phương ơi ! Cái dòng \(P=\)cuối ấy . Chỗ đấy là \(\ge-1\)em nhé!

đề sai ko thể nào là GTNN

Lớn nhất

D = -x² - 8x + 7 = - (x² + 8x - 7) = - (x² + 8x + 16) + 23 = 23 - (x + 4)²

*) (x + 4)² \(\ge\)0

Vậy giá trị lớn nhất của D = 23 tại x = -4

-20 chắn chắn

Thank . Nhưng sai rồi đó bạn