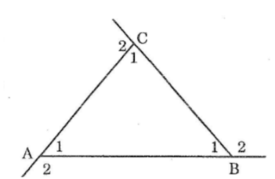
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)

∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)

∠(C1 ) +∠(C2 )=180o(hai góc kề bù)

Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o

⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)

Trong ΔABC, ta có:

∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)

Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o

Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có:
A^1 + A^2 = 180⁰
B^1 + B^2 = 180⁰
C^1 + C^2 = 180⁰
---------------------
Cộng vế theo vế được:
A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180⁰
mà A^1 +B^1 +C^1 = 180⁰ (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.180⁰ - 180⁰ = 2.180⁰ = 360⁰

 Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC. 
Ta có: 
A^1 + A^2 = 180* 
B^1 + B^2 = 180* 
C^1 + C^2 = 180* 
--------------------- 
Cộng vế theo vế được: 
A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180* 
mà A^1 +B^1 +C^1 = 180* (tổng 3 góc trong của tam giác) 
=> A^2 +B^2 +C^2 = 3.180* - 180* = 2.180* = 360*

Ta có:  góc ngoài của một tam giác bằng tổng 2 góc trong ko kề với nó

=> Tổng 3 góc ngoài của 1 tam giác bằng tổng 2 lần các góc trong ko kề với nó

Mà tổng 2 lần các góc trong ko kề với nó = 2 x (tổng 3 góc của 1 tam giác) = 2 x 180⁰ = 360⁰

Vậy tổng ba góc ngoài ở ba đỉnh của một tam giác bằng 360⁰

Vẽ tam giác ABC bất kì, có ˆA1,ˆB1,ˆC1A1^,B1^,C1^ lần lượt là các góc trong tại các đỉnh A, B, C và ˆA2,ˆB2,ˆC2A2^,B2^,C2^ lần lượt là các góc ngoài tại các đỉnh A, B, C của$△ABC$. 
Theo định lí: Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó. 
Ta có: ˆA2=ˆB1+ˆC1A2^=B1^+C1^ ˆB2=ˆA1+ˆC1B2^=A1^+C1^ ˆC2=ˆA1+ˆB1C2^=A1^+B1^ 
\Rightarrow ˆA2+ˆB2+ˆC2=ˆA1+ˆB1+ˆC1+ˆA1+ˆB1+ˆC1A2^+B2^+C2^=A1^+B1^+C1^+A1^+B1^+C1^ 
\Rightarrow ˆA2+ˆB2+ˆC2=2.ˆA1+

\(A+A_1+B+B_1+C+C_1=3.180\)

Mà A+B+C=180=> \(A_1+B_1+C_1=360\)

Câu hỏi tương tự nha ! Kéo xuống là thấy !!! 

tích nha

vì một góc ngoài bằng tổng 2 góc trong cộng lại thì 3 góc ngoài nhân lên bằng 360⁰(tick nha)