cho tam giác ABC qua A kẻ đường thẳng xy bất kì không cắt các cạnh của tam giác ABC, kẻ BD, CE vuông góc với xy. Chứng minh rằng đường trung trực của đoạn thẳng DE luôn đi qua 1 điểm cố định

Những câu hỏi liên quan
cho tam giác ABC có Góc A bằng 90 độ, AB=AC. Qua đỉnh A kẻ đường thẳng xy sao cho không cắt đoạn thẳng BC. Kẻ BD và CE vuông góc với xy ( D,E thuộc xy ). Chứng minh rằng:
a) Tam giác ABD=Tam giác CAE.
b) DE=BD+CE
Do xy không cắt đoạn BC
=> xy //BC
=> ECBD là hình chữ nhật'
Xét \(\Delta ABD\)và \(\Delta ACE\)có: \(\hept{\begin{cases}AB=AC\left(gt\right)\\\widehat{AEC}=\widehat{ADB}=90^o\\EC=BD\end{cases}}\)
=> \(\Delta ABD=\Delta ACE\)
=> AE=AD
=> Tam giác ADE cân tại E
\(\widehat{ACB}=45^o\Rightarrow\widehat{ECA}=45^o\)
=> EC=EA
Tương tự: AD=BD
=> DE=AE+AD=EC+BD
a, Xét \(\Delta\)ABD và \(\Delta\)ACE ta cs :
AB = AC (gt)
^AEC = ^ADB = 900
CE = BD (gt)
=> \(\Delta\)ABD = \(\Delta\)ACE
b, Ta có xy không cắt BC
=> xy//BC
=> ^DBA= ^DAB (vị trí đồng vị)
=> \(\Delta\) BDA cân tại D
=> DA=DB
\(\Delta\)EAC cân tại E (cmt)
=> EA=EC
=> DE = AD + AC = BD + CE
Bài 1: Cho tam giác ABC vuông tại A. Qua A kẻ đường thẳng xy sao cho xy tạo với AB góc BAx 45 độ( Góc BAx nằm ngoài tam giác ABC). Từ B và C hạ BK vuông góc với xy, CI vuông góc với xy, M là trung điểm của BC. Chứng minh:a) MI và MK lần lượt là trung trực của AC và AB b) Góc IMK vuôngBài 2: Cho tam giác ABC có góc A tù. Tia phân giác của góc B và góc C cắt nhau tại O. Lấy điểm E trên cạnh AB. Từ E hạ EP vuông góc với BO và từ P hạ PF vuông góc với OC( P thuộc BC và F thuộc AC). Chứng minh rằng:...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A. Qua A kẻ đường thẳng xy sao cho xy tạo với AB góc BAx = 45 độ( Góc BAx nằm ngoài tam giác ABC). Từ B và C hạ BK vuông góc với xy, CI vuông góc với xy, M là trung điểm của BC. Chứng minh:
a) MI và MK lần lượt là trung trực của AC và AB
b) Góc IMK vuông
Bài 2: Cho tam giác ABC có góc A tù. Tia phân giác của góc B và góc C cắt nhau tại O. Lấy điểm E trên cạnh AB. Từ E hạ EP vuông góc với BO và từ P hạ PF vuông góc với OC( P thuộc BC và F thuộc AC). Chứng minh rằng: Khi E di động trên cạnh AB thì đường trung trực của EF luôn đi qua 1 điểm cố định
ai nhanh cho 1 tick
Cho tam giác ABC vuông tại A và AB = AC. Qua đỉnh A kẻ đường thẳng xy sao cho xy không cắt đoạn thẳng BC. Kẻ BD và CE vuông góc với xy ( D ∈ xy, E ∈ xy ).Chứng minh
a) Góc DAB = Góc ACE
b) ∆ABD = ∆CAE
c) DE = BD + CE
Bạn kham khảo câu này nhé dù không làm nhưng bạn có thể cho mình 1 tk được ko.
Câu hỏi của Trịnh Tuấn Tú - Toán lớp 7 - Học toán với OnlineMath
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, C nằm cùng phía đối với xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng: DE = BD + CE
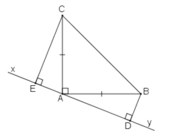
Ta có: ΔAEC= ΔBDA
⇒AE = BD và EC = DA
Mà DE = DA + AE
Vậy: DE = CE + BD
Đúng 2
Bình luận (0)
cho tam giác ABC có góc A =90độ và AB=AC. qua đỉnh A kẻ đường thẳng xy sao cho xy không cắt đoạn thẳng BC. Kẻ BD và CE vuông góc vs xy. CMR:
a) CM tam giác ABD = tam giác CAE
b) DE = BD + CE
Câu 4:
Cho tam giác ABC cân tại A; điểm D thuộc cạnh BC; điểm E thuộc tia đối tia CB sao cho BD= CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt đường thẳng AB; AC tại M; N. Chứng minh rằng:
a) DM= EN ; AD> DM
b) MN cắt BC tại trung điểm của MN
c) Đường trung trực của MN luôn đi qua 1 điểm cố định khi D thay đổi trên cạnh BC
Cho tam giác ABC có A=90độ. Qua A kẻ đường thẳng xy ( B,C nằm cùng phía với xy). Kẻ BD và CE vuông góc với xy. Chứng minh rằng
a) tam giác BAD= tam giác ACE
b) DE=BD+CE
Cho tam giác ABC có a^ =90độ .Qua đỉnh a kẻ đường thẳng xy sao cho k cắt BC .Kẻ bd và ce vuông góc vs xy .chứng minh rằng:
a) tam giác abd= ta giác ace
b)de=bd+ce
Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy sao cho B, C nằm cùng phía với xy. Kẻ BD và CE vuông góc với xy.
a) Chứng minh: DE = BD + CE;
b) Gọi M là trung điểm của BC. Lấy N là một điểm trên đoạn thẳng MC. Kẻ BP và CQ vuông góc với tia AN. Chứng minh PQ = BP - CQ.
a) Xét ∆BAD và ∆ACE có:
^BDA=^AEC (cùng bằng 90 độ)
AB=AC (gt)
^BAD=^ACE (cùng phụ với ^EAC)
suy ra ∆BAD=∆ACE (cạnh huyền-góc nhọn)
b) Do ∆BAD=∆ACE nên AD=CE và AE=BD
mà DE=DA+AE
suy ra DE = CE+BD (đpcm)
Đúng 0
Bình luận (0)
b) Có: BAP + PAC = 90o
t/g BPA vuông tại P có: ABP + BAP = 90o
Suy ra PAC = ABP
Xét t/g BPA vuông tại P và t/g AQC vuông tại Q có:
AB = AC (gt)
ABP = CAQ (cmt)
Do đó, t/g BPA = t/g AQC ( cạnh huyền - góc nhọn)
=> AP = QC (2 cạnh tương ứng)
và BP = AQ (2 cạnh tương ứng)
= AP + PQ = QC + PQ
=> PQ = BP - QC (đpcm)
Đúng 1
Bình luận (0)



















