Áp dụng HDT
4x2 -9
Những câu hỏi liên quan
Xét sự biến thiên của hàm số
y
4
x
+
5
+
x
−
1
trên tập xác định của nó. Áp dụng tìm số nghiệm của phương trình
4
x
+
5
+
x
−
1
4
x
2
+...
Đọc tiếp
Xét sự biến thiên của hàm số y = 4 x + 5 + x − 1 trên tập xác định của nó. Áp dụng tìm số nghiệm của phương trình 4 x + 5 + x − 1 = 4 x 2 + 9 + x
A. 1 nghiệm duy nhất
B. 2 nghiệm
C. 3 nghiệm
D. Vô nghiệm
Áp dụng công thức nghiệm để giải các phương trình: 4x2 – 4x + 1 = 0
4x2 – 4x + 1 = 0;
a = 4; b = -4; c = 1
Δ = b2 - 4ac = (-4)2 - 4.4.1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
Đúng 0
Bình luận (0)
bài 4:áp dụng hằng đẳng thức đáng nhớ
a,(x-1).(x2+x+1)
b,(x-5).(x2+5x+25)
c,(2x+3).(4x2-6x+9)
d,(x+1/2).(x2-1/2x+1
giúp với ạ đang cần gấp
Áp dụng công thức nghiệm để giải các phương trình:
a
)
5
x
2
−
x
+
2
0
b
)
4
x
2
−
4
x...
Đọc tiếp
Áp dụng công thức nghiệm để giải các phương trình:
a ) 5 x 2 − x + 2 = 0 b ) 4 x 2 − 4 x + 1 = 0 c ) − 3 x 2 + x + 5 = 0
a) 5 x 2 – x + 2 = 0 ;
a = 5; b = -1; c = 2
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 5 . 2
= 1 - 40 = -39 < 0
Vậy phương trình trên vô nghiệm.
b) 4 x 2 – 4 x + 1 = 0 ;
a = 4; b = -4; c = 1
Δ = b 2 - 4 a c = ( - 4 ) 2 - 4 . 4 . 1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
c) - 3 x 2 + x + 5 = 0
a = -3; b = 1; c = 5
Δ = b 2 - 4 a c = 12 - 4 . ( - 3 ) . 5 = 1 + 60 = 61 > 0
⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt
x 1 = ( 1 - √ 61 ) / 6 ; x 2 = ( 1 + √ 61 ) / 6
Đúng 0
Bình luận (0)
Áp dụng HDT
a) -16a4b6 - 24a5b5 - 9a6b4
b) x2/4 + 2xy + 4y2
b) \(\left(\frac{x}{2}\right)^2\)+2.\(\frac{x}{2}\).2y+\(\left(2y\right)^2\)
=\(\left(\frac{x}{2}+2y\right)^2\)
Đúng 0
Bình luận (0)
1:áp dụng quy tắc đối đầu hay thực hiện phép tính cộng
2x+1/2x2-x + 32x2/1-4x2 +1-2x/2x2+x
2:tính
a,4x2/x-2 +3/x-2 +19/2-x
b,2x/x2+2xy +y/xy-2y2 +4/x2-4y2
Bài 2:
a: \(=\dfrac{4x^2+3-19}{x-2}=\dfrac{4x^2-16}{x-2}=\dfrac{4\left(x-2\right)\left(x+2\right)}{x-2}=4x+8\)
b: \(=\dfrac{2x}{x^2+2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)
\(=\dfrac{2}{x+2y}-\dfrac{1}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2x-4y-x-2y+4}{\left(x+2y\right)\left(x-2y\right)}\)
\(=\dfrac{x-6y+4}{\left(x+2y\right)\left(x-2y\right)}\)
Đúng 0
Bình luận (0)
1:áp dụng quy tắc đối đầu hay thực hiện phép tính cộng
2x+1/2x2-x + 32x2/1-4x2 +1-2x/2x2+x
2:tính
a,4x2/x-2 +3/x-2 +19/2-x
b,2x/x2+2xy +y/xy-2y2 +4/x2-4y2
Bằng cách sử dụng hằng đẳng thức a2 - b2 (a - b)(a + b) hãy xét dấu f(x) x4 - x2 + 6x - 9 và
g
x
x
2
-
2
x
-
4
x
2
-
2...
Đọc tiếp
Bằng cách sử dụng hằng đẳng thức a2 - b2 = (a - b)(a + b) hãy xét dấu f(x) = x4 - x2 + 6x - 9 và g x = x 2 - 2 x - 4 x 2 - 2 x
Ta có:
f(x) = x4 – x2 + 6x – 9 = x4 – (x2 – 6x +9) = – (x-3)2
= (x2 –x + 3).(x2 + x - 3)
+ Tam thức x2 – x + 3 có Δ = -11 < 0, a = 1 > 0 nên x2 – x + 3 > 0 với ∀ x ∈ R.
+ Tam thức x2 + x – 3 có hai nghiệm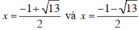 
Ta có bảng xét dấu sau:
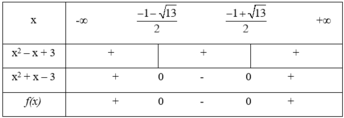
Kết luận:
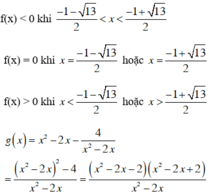
Tam thức x2 - 2x + 2 có Δ = -4 < 0, hệ số a = 1 > 0 nên x2 - 2x + 2 > 0 với ∀ x ∈ R
Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3.
Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2
Ta có bảng xét dấu :
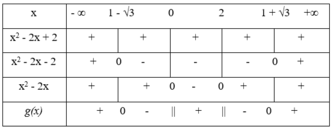
Kết luận : g(x) < 0 khi x ∈ (1 - √3; 0) ∪ (2; 1 + √3)
g(x) = 0 khi x = 1- √3 hoặc x = 1 + √3
g(x) > 0 khi x ∈ (-∞; 1 - √3) ∪ (0; 2) ∪ (1 + √3; +∞)
g(x) không xác định khi x = 0 và x = 2.
Đúng 0
Bình luận (0)
(4x2+2x-18)2-(4x2+2x)2 =M.(4x2+2x-9)
Mấy bạn giúp mình nha !
\(\Leftrightarrow M\cdot\left(4x^2+2x-9\right)=\left(4x^2+2x-18-4x^2-2x\right)\left(4x^2+2x-18+4x^2+2x\right)\)
\(\Leftrightarrow M\cdot\left(4x^2+2x-9\right)=-18\cdot\left(8x^2+4x-18\right)\)
\(\Leftrightarrow M=-18\cdot2=-36\)
Đúng 1
Bình luận (0)