Cho tam giác ABC có góc A = 60 độ, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, Vẽ điểm E đối xứng với M qua AC
a/ Chứng minh tam giác ADE cân
b/ Tính góc ADE
Cho tam giác ABC có góc B bằng 70 độ, điểm M thuộc cạnh AC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua BC. Chứng minh rằng tam giác BDE cân và tính góc DBE
Cho tam giác ABC có góc B bằng 70 độ, điểm M thuộc cạnh AC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua BC. Chứng minh rằng tam giác BDE cân và tính góc DBE
Toán lớp 8a) M đối xứng với D qua AB nên MB=BD và AB vuông góc với MD. Ta thấy Am vừa là đường trung tuyến vừa là đường trung trực nên tam giác AMD cân ở A nên AM=AD
Tương tự ta chứng minh được tam giác AEM cân ở A nên AM=AE
=>AE=AD=AM
b)Gọi I là điểm giao của AB và MD, K là giao của AC và ME
tam giác AMD cân có AB là đường trung trực nên cũng là đường phân giác của góc MAD nên góc DAB=gócBAM
tam giác MAE cũng vậy nên góc MAC=gócEAC
vậy góc DAE=góc DAB+ góc BAM + góc MAC +góc CAE
= 2 (góc BAM+ goc MAC)
=2.70
=140 độ
Cho tam giác ABC có: góc A=60o, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua Ab, vẽ điểm E đối xứng với M qua AC.
a, CMR: Tam giác ADE cân, b, Tính góc ADE
Cho tam giác ABC nhọn. M là điểm bất kì trên cạnh BC. D đối xứng với M qua AB, E đối xứng với M qua AC. DE cắt AB và AC lần lượt tại I và K.
a) Chứng minh tam giác ADE cân
b) Chứng minh MA là tia phân giác của góc IMK
c) Biết góc BAC bằng 70 độ .Tính các góc của tam giác ADE
a. Ta có \(M,D\) đối xứng qua \(AB\)
\(\rightarrow AD=AM\)
Lại có \(M,E\) đối xứng qua \(AC\rightarrow AM=AE\)
\(\rightarrow AD=AE\rightarrow\Delta ADE\) CÂN
b. Ta có \(M,D\) đối xứng qua \(AB,I\in AB\)
\(\rightarrow\widehat{IMA}=\widehat{IDA}=\widehat{ADE}\)
Tương tự \(\widehat{KMA}=\widehat{KEA}=\widehat{DEA}\)
Mà \(\Delta ADE\) cân tại \(A\)
\(\rightarrow\widehat{ADE}=\widehat{AED}\)
\(\rightarrow\widehat{IMA}=\widehat{KMA}\)
\(\rightarrow MA\) là phân giác \(\widehat{IMK}\)c. Ta có \(M,D\) đối xứng qua \(AB\)\(\rightarrow\widehat{DAB}=\widehat{BAM}\rightarrow\widehat{DAM}=2\widehat{BAM}\)Tương tự \(\widehat{MAE}=2\widehat{MAC}\)\(\rightarrow\widehat{DAE}=\widehat{DAM}+\widehat{MAE}\)\(\rightarrow\widehat{DAE}=2\widehat{BAM}+2\widehat{MAC}=2\widehat{BAC}=140^o\)\(\rightarrow\widehat{ADE}=\widehat{AED}=90^o-\frac{1}{2}\widehat{DAE}=20^o\)Cho tam giác ABC có góc A = 70^o , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. a. Chứng minh rằng AD = AE b. Tính số đo góc DAE
tự kẻ hình :
AB là đường trung trực của MD (gt)
=> AM = AD (đl) (1)
AC là đường trung trực của EM (gt)
=> AE = AM (đl) (2)
(1)(2) => AE = AD
a. Vì D đối xứng với M qua trục AB
\(\Rightarrow\) AB là đường trung trực MD.
\(\Rightarrow\) AD = AM (tính chất đường trung trực) (1)
\(\Rightarrow\) Vì E đối xứng với M qua trục AC
\(\Rightarrow\) AC là đường trung trực của ME
\(\Rightarrow\) AM = AE ( tính chất đường trung trực) (2)
\(\Rightarrow\) Từ (1) và (2) suy ra : AD = AE
b ) AD = AM suy ra \(\Delta AMD\) cân tại A có \(AB\perp MD\)
nên AB cũng là đường phân giác của góc MAD
\(\Rightarrow\widehat{A_1}=\widehat{A}_2\)
AM = AE suy ra \(\Delta AME\) cân tại A có \(AC\perp ME\) nên AC cũng là đường phân giác của \(\widehat{MAE}\)
\(\Rightarrow\widehat{A}_3=\widehat{A}_4\)
\(\widehat{DAE}=\widehat{A}_1+\widehat{A}_2+\widehat{A}_3+\widehat{A}_4\)
\(=2\left(\widehat{A}_2+\widehat{A}_3\right)=2\widehat{BAC}=2.70^o=140^o\)
Chúc bạn học tốt !!!
cho tam giác ABC có góc A = 70 độ ,điểm M thuộc cạnh BC . Vẽ điểm D đối xứng với M qua AB , vẽ điểm E đối xứng với M qua AC .
a) chứng minh rằng AD =AE
b) tính số đo góc DAE
Cho tam giác ABC có góc A=70o, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC
a) Chứng minh rằng AD=AE
b) tính số đo góc DAE
a: Ta có: D đối xứng với M qua AB
nên AD=AM(1)
Ta có: E đối xứng với M qua AC
nên AM=AE(2)
Từ (1) và (2) suy ra AD=AE
1) Cho tam giác nhọn ABC, M thuộc BC. gọi D và E lần lượt là điểm đối xứng của M qua AB, AC.
a) Chứng minh: tam giác ADE cân
b) DE cắt AB và AC theo thứ tự tại I,K. Chứng minh: MA kaf tia phân giác góc IMK
c) Biết góc BAC= 70 độ. Tính các góc của tam giác ADE
2) Cho tam giác đều ABC. Trọng tâm G. Gọi M là điểm đối xứng với G qua BC. Chứng minh:
a) tam giác BGC= tam giác BMC
b) tính các góc trong tam giác BMC
1.Cho hình thang vuông ABCD (góc A bằng góc B bằng 90 độ). M là trung điểm đối xứng với B qua AD, I là giao điểm của CH và AD. Chứng minh góc AIB = góc DIC
2.Cho A nhọn tam giác ABC có góc A bằng 60 độ, trực tâm H. M là điểm đối xứng qua BC. Chứng minh tam giác BHC bằng tam giác BMC
3. Cho tam giác ABC cân tại A. M là trung điểm của BC. Trên AB lấy điểm D, trên AC lấy điểm E sao cho BD bằng CE
4. Cho tam giác nhọn ABC có góc A bằng 70 độ, điểm D thuộc BC. E là điểm đối xúng với D qua AB, F là điểm đối xứng với D qua AC. Đường thẳng EF cắt AB và AC, theo thứ tự tại M, N. Tính các góc của tam giác AEF ?
Các bạn vẽ hình cho mình với nha
Cho tam giác ABC có ∠ A = 70 0 , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Tính số đo góc ∠(DAE)
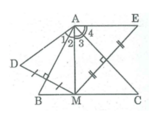
AD = AM suy ra ∆ AMD cân tại A có AB ⊥ MD nên AB cũng là đường phân giác của ∠ (MAD)
⇒ ∠ A 1 = ∠ A 2
AM = AE suy ra ∆ AME cân tại A có AC ⊥ ME nên AC cũng là đường phân giác của ∠ (MAE)
⇒ ∠ A 3 = ∠ A 4
∠ (DAE) = ∠ A 1 + ∠ A 2 + ∠ A 3 + ∠ A 4 = 2( ∠ A 2 + ∠ A 3 ) = 2 ∠ (BAC) = 2. 70 0 = 140 0