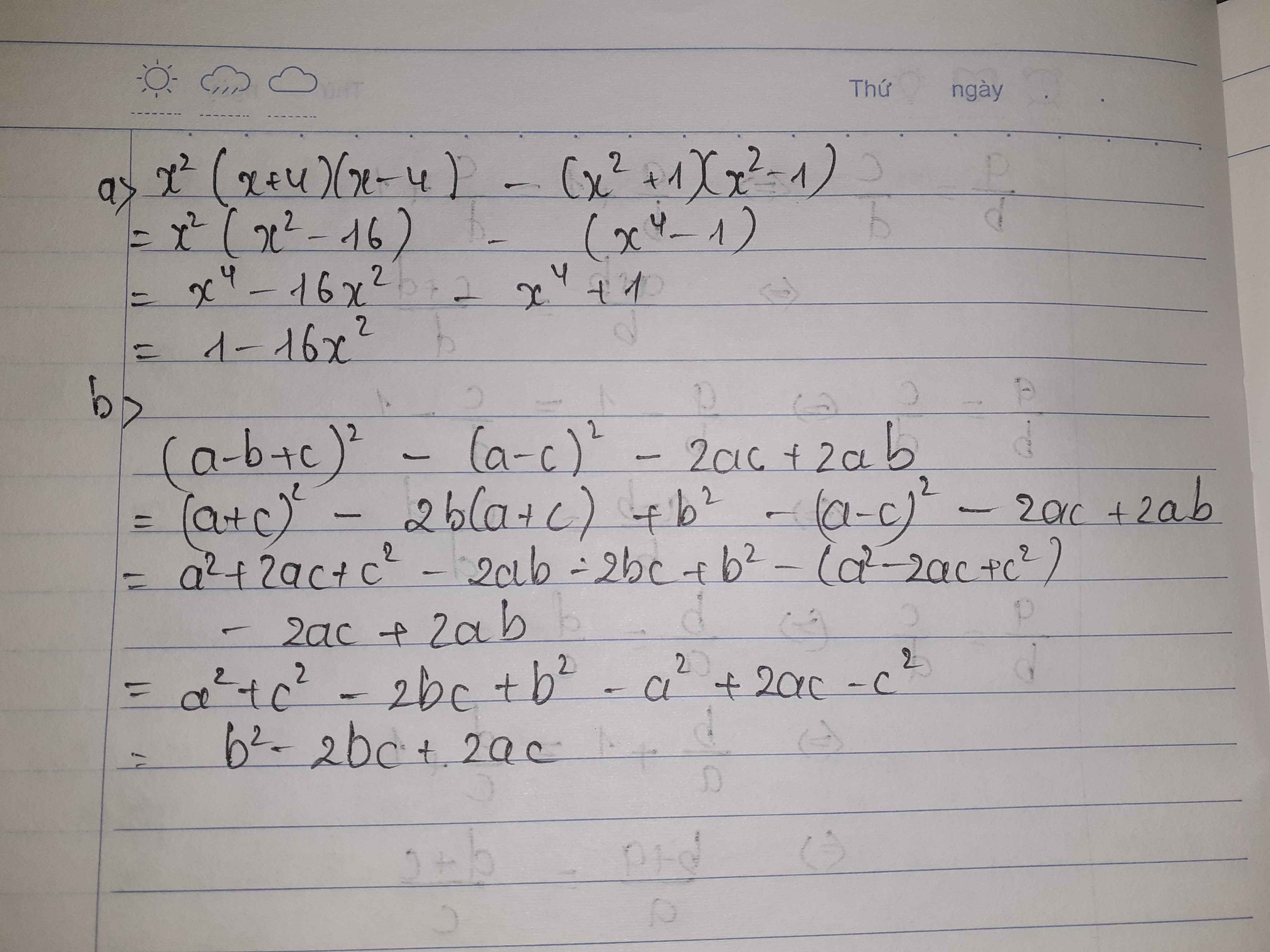rút gọn: p=(a^2 - 2ab + b^2) x ( a^2 + 2ab + b^2)

Những câu hỏi liên quan
Rút gọn P = 2x-y-{2x-y-[y+3x-(5y-x)]} với x = a2+2ab+b2 , y=a2-2ab+b2
\(\frac{a^2+b^2-c^2+2ab}{a^2-b^2+c^2+2ab}\)
Rút gọn biểu thức
Rút gọn A=\(\frac{a^2+2ab+b^2}{a}.\left(\frac{a}{a^2+2ab+b^2}-\frac{a}{a^2-b^2}\right)+\frac{5a-3b}{a-b}\)
Rút gọn biểu thức:
2y - x - {2x - y - [y + 3x - (5y - x)]}
với x = a2 + 2ab + b2 , y = a2 - 2ab + b2
Rút gọn biểu thức:
2y - x - {2x - y - [y + 3x - (5y - x)]}
với x = a2 + 2ab + b2 , y = a2 - 2ab + b2
Rút gọn:
a. x(x+4)(x-y)-(x^2-y)(x^2-1)
b.(y-3)(y+3)(y^2+9)-(y^2+2)(y^2-2)
c.(a+b-c)-(a-c)^2-2ab+2ab
d.(a+b+c)^2+(b+c-a)^2+(c+a-b)^2+(a+b-c)^2
Cho A = 3y-2x+{3x-2y-[y+2x(5x+y]-4(2x-5y)}
Rút gọn A, biết
x=a2-2ab+b2 và y=a2+2ab+b2
Rút gọn: \(A=\frac{3a^2-2ab-b^2}{2a^2+ab-b^2}:\frac{3a^2-4ab+b^2}{3a^2+2ab-b^2}\)
bạn có thể phân tích thành nhân tử rồi rút gọn
vd: như tử của cái bên trái ta tách đc thế này: 3a^2-3ab+ab-b^2 bằng 3a(a-b)+b(a-b) bằng (3a+b)(a-b) chẳng hạn là vậy
Chúc bạn giải thành công!:))
Đúng 0
Bình luận (0)
\(A=\frac{3a^2-2ab-b^2}{2a^2+ab-b^2}:\frac{3a^2-4ab+b^2}{3a^2+2ab-b^2}\)
\(=\frac{3a^2-2ab-b^2}{2a^2+ab-b^2}.\frac{3a^2+2ab-b^2}{3a^2-2ab-b^2}\)
\(=\frac{\left(3a^2-2ab-b^2\right)\left(3a^2+2ab-b^2\right)}{\left(2a^2+ab-b^2\right)\left(3a^2-2ab-b^2\right)}\)
\(=\frac{9a^4+6a^3b-3a^2b^2-6a^3b-4a^2b^2+2ab^3-3a^2b^2-2ab^3+b^4}{6a^4-4a^3b-2a^2b^2+3a^3b-2a^2b^2-ab^3-3a^2b^2+2ab^3+b^4}\)
\(=\frac{9a^4-10a^2b^2+b^4}{6a^4-a^3b-7a^2b^2+ab^3+b^4}\)
\(=\frac{9a^4-9a^2b^2-a^2b^2+b^4}{6a^4-6a^2b^2-a^2b^2+b^4-a^3b+ab^3}\)
\(=\frac{9a^2\left(a^2-b^2\right)-b^2\left(a^2-b^2\right)}{6a^2\left(a^2-b^2\right)-b^2\left(a^2-b^2\right)-ab\left(a^2-b^2\right)}\)
\(=\frac{\left(a^2-b^2\right)\left(9a^2-b^2\right)}{\left(a^2-b^2\right)\left(6a^2-b^2-ab\right)}\)
\(=\frac{9a^2-b^2}{6a^2-b^2-ab}\)
\(=\frac{\left(3a-b\right)\left(3a+b\right)}{6a^2-3ab+2ab-b^2}\)
\(=\frac{\left(3a-b\right)\left(3a+b\right)}{3a\left(a-b\right)+2b\left(a-b\right)}\)
\(=\frac{\left(3a-b\right)\left(3a+b\right)}{\left(a-b\right)\left(3a+2b\right)}\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức
a)x^2(x+4)(x-4)-(x^2+1)(x^2-1)
b) (a-b+c)^2-(a-c)^2-2ac+2ab
`a)x^2(x+4)(x-4)-(x^2+1)(x^2-1)`
`=x^2(x^2-16)-(x^2+1)(x^2-1)`
`=x^4-16x^2-(x^4-1)`
`=-16x^2+1`
`b) (a-b+c)^2-(a-c)^2-2ac+2ab`
`=a^2+b^2+c^2-2ab-2bc+2ac-(a^2-2ac+c^2)-2ac+2ab`
`=a^2+b^2+c^2-2ab-2bc+2ac-a^2+2ac-c^2-2ac+2ab`
`=b^2-2bc+2ac`
Đúng 1
Bình luận (0)
a) Ta có: \(x^2\left(x+4\right)\left(x-4\right)-\left(x^2+1\right)\left(x^2-1\right)\)
\(=x^2\left(x^2-16\right)-\left(x^4-1\right)\)
\(=x^4-16x^2-x^4+1\)
\(=-16x^2+1\)
b) Ta có: \(\left(a-b+c\right)^2-\left(a-c\right)^2-2ac+2ab\)
\(=\left(a-b+b-a+c\right)\left(a-b+c+a-c\right)-2ac+2ab\)
\(=c\left(2a-b\right)-2ac+2ab\)
\(=2ac-2bc-2ac+2ab\)
\(=2ab-2bc\)
Đúng 1
Bình luận (0)