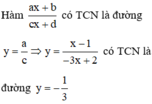cho y=x³-8/(x²-3x+2)(x²-9) số tiệm cận của hàm số là

Những câu hỏi liên quan
26. Tìm số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số y = \(\dfrac{\sqrt{x-1}}{x^2-3x+2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ
Đúng 1
Bình luận (0)
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
x
+
3
x
-
1
x
2
-
1
là A. 1. B. 2. C. 3 D. 4.
Đọc tiếp
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = x + 3 x - 1 x 2 - 1 là
A. 1.
B. 2.
C. 3
D. 4.
Gọi số
n
∈
N
là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
x
+
1
x
2
-
3
x
+
2
. Tìm n A.1 B.0 C. 2 D. 3
Đọc tiếp
Gọi số n ∈ N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x + 1 x 2 - 3 x + 2 . Tìm n
A.1
B.0
C. 2
D. 3
Số đường tiệm cận của đồ thị hàm số y = 3 x - 1 x 2 + x + 2 là
A. 0
B. 3
C. 1
D. 2
Đáp án D
Ta có

Vậy y = 3 là một tiệm cận ngang của đồ thị hàm số.

Vậy y = −3 là một tiệm cận ngang của đồ thị hàm số.
Đúng 0
Bình luận (0)
Số đường tiệm cận của đồ thị hàm số
y
3
x
−
1
x
2
+
x
+
2
là A. 1 B. 0 C. 2 D. 3
Đọc tiếp
Số đường tiệm cận của đồ thị hàm số y = 3 x − 1 x 2 + x + 2 là
A. 1
B. 0
C. 2
D. 3
Gọi số n thuộc N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
x
+
1
x
2
-
3
x
+
2
Tìm n A.1 B.0 C. 2 D. 3
Đọc tiếp
Gọi số n thuộc N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x + 1 x 2 - 3 x + 2 Tìm n
A.1
B.0
C. 2
D. 3
Tiệm cận đứng của đồ thị hàm số y = x - 2 x 2 - 3 x + 2 là
A. x=2.
B. x=1.
C. x=0.
D. x=1 và x=2.
Tiệm cận ngang của đồ thị hàm số
y
x
−
1
−
3
x
+
2
là? A.
x
2
3
B.
y
2
3
C.
x
−...
Đọc tiếp
Tiệm cận ngang của đồ thị hàm số y = x − 1 − 3 x + 2 là?
A. x = 2 3
B. y = 2 3
C. x = − 1 3
D. y = − 1 3
Tiệm cận ngang của đồ thị hàm số
y
x
−
1
−
3
x
+
2
là? A.
y
−
1
3
B.
x
2
3
C.
y...
Đọc tiếp
Tiệm cận ngang của đồ thị hàm số y = x − 1 − 3 x + 2 là?
A. y = − 1 3
B. x = 2 3
C. y = 2 3
D. x = − 1 3