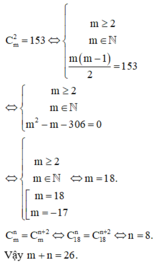Tìm n thỏa mãn:
1+2+3+.............+n=153
Tìm n thỏa mãn:1+2+3+...+n=153
1+2+3+...+n=153
=>(n+1).n:2=153
=>(n+1).n=153.2
=>(n+1).n=306
mà 306=(17+1).17
=>(n+1).n=(17+1).17
=>n=17
tìm chữ sỗ n thỏa mãn 1+2+3+........+n=153 - Giúp tôi giải ...
Số các số hạng của dãy là: \(\frac{n-1}{1}+1=n\)(số hạng)
Ta có: \(\frac{\left(n+1\right)n}{2}=153\Rightarrow\left(n+1\right)n=306\)
Vì (n+1) và n là 2 số tự nhiên liên tiếp có tích bằng 306 mà 306=17*18 suy ra: n=17
Tìm n thỏa mãn : 1 + 2 + 3 + ... + n = 153
1+2+3....+n=153
<=>[n.(n+1)]:2=153
<=>n.(n+1)=153.2=306=17.18=17.(17+1)
=>n=17
Vậy n=17 thỏa mãn
1 + 2 + 3 + .... + n = 153
=> [ n.( n + 1 ) ] : 2 = 153
=> n.( n + 1 ) = 153 . 2
=> n.( n + 1 ) = 306 = 17 . 18
=> n.( n + 1 ) = 17.( 17 + 1 )
=> n = 17
ta có công thức tính dãy số này là 1+2+3+...+n=n(n+1)/2
theo đề ta có: 1+2+3+...+n=n(n+1)/2=153
=> n=17 (đoạn kia tự giải nghe)
tìm chữ sỗ n thỏa mãn 1+2+3+........+n=153
1+2+3+...+n=153
=>(n+1).n:2=153
=>(n+1).n=153.2
=>(n+1).n=306
mà 306=(17+1).17
=>(n+1).n=(17+1).17
=>n=17
Tìm n thỏa mãn:1+2+3+...+n=153
Trả lời n=
tìm n thỏa mản:1+2+3+...+n=153
1+ 2+ 3+ ...+ n= 153
Số số hạng của tổng là:
(n- 1)+ 1= n (số hạng)
Tổng là: \(\frac{\left(n+1\right)\times n}{2}\)= 153
=> (n+ 1) x n= 153. 2
=> (n+ 1) x n= 306
Mà 18. 17= 306
Vậy n= 17
Tick mình nhé!
Tìm n thõa mãn: 1+2+3+...+n=153
Trả lời: n=
Ta có :
153=1+2+3+4+.....+n=(n+1)x n :2
=> (n+1) x n =153 x 2=306
...........................
n =17
các bn giúp mình giải 1 số bài tập này nhé :
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho n-2
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho 2n -2
-tìm các số nguyên x thỏa mãn x lớn hơn hoặc bằng -21/7 và x bé hơn hoặc bằng 3
-tìm các số tự nhiên x,y thỏa mãn x-1 chia hết cho y , y-1 chia hết cho x
Cho các số tự nhiên m, n thỏa mãn đồng thời các điều kiện C m 2 = 153 và C m n = C m n + 2 Khi đó m+n bằng
A. 25
B. 27
C. 26
D. 23
Cho các số tự nhiên m, n thỏa mãn đồng thời các điều kiện C m 2 = 153 và C m n = C m n + 2 . Khi đó m+n bằng
A. 25
B. 27
C. 26
D. 23
Chọn C.
Phương pháp: Giải các phương trình đã cho.
Cách giải: Ta có: