Tìm tập xác định của hàm số
\(y=\frac{cotx}{1+3sin^2x}\)
Những câu hỏi liên quan
1.Tìm tập xác định của các hàm số sau:
a. y =\(\frac{1}{\sqrt{-cotx-\sqrt{3}}}\)
b. y = \(\frac{1}{cotx-\sqrt{3}}\)
Xét bốn mệnh đề sau:
1
: Hàm số
y
s
inx
có tập xác định là
R
2
: Hàm số
y
c
osx
có tập xác định là
R
3
Hàm số
y
tan
x
có tập xác định là
R
4
Hàm số
y
cot...
Đọc tiếp
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số: y = c o t x + π 6
Hàm số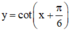 
xác định
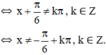
Vậy tập xác định của hàm số là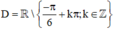 
Đúng 0
Bình luận (0)
Tập xác định của hàm số y = cotx là
Tập xác định của hàm số: y = cotx là:
Tập xác định của hàm số y cotx là A. B. C. D.
Đọc tiếp
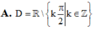
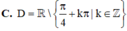
Tập xác định của hàm số y = cotx là
A.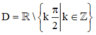 
B. 
C. 
D. 
Chọn B
Hàm số đã cho xác đinh khi sinx ≠ 0 ⇔ x ≠ k π ( k ∈ ℤ )
Đúng 0
Bình luận (0)
Tập xác định của hàm số
y
c
o
t
x
là
Đọc tiếp
Tập xác định của hàm số y = c o t x là
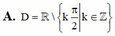
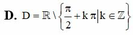
Tập xác định của hàm số y = tan x + c o t x là
A. R
Giúp mình với ạ. Mọi người biết câu nào thì giải chi tiết giúp mình với (vì vào học chậm hơn các bạn nên ko hiểu gì hết ạ). Cảm ơn mn nhiều lắm.Tìm tập xác định của hàm sốa) yfrac{3sinx+5}{1+tan^2X}b) y frac{2-cotx}{1+cos2x}c) y frac{1}{cotx-sqrt{3}}d) y frac{sinx}{1-2sin^2x}
Đọc tiếp
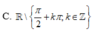
Giúp mình với ạ. Mọi người biết câu nào thì giải chi tiết giúp mình với (vì vào học chậm hơn các bạn nên ko hiểu gì hết ạ). Cảm ơn mn nhiều lắm.
Tìm tập xác định của hàm số
a) y=\(\frac{3sinx+5}{1+tan^2X}\)
b) y= \(\frac{2-cotx}{1+cos2x}\)
c) y= \(\frac{1}{cotx-\sqrt{3}}\)
d) y= \(\frac{sinx}{1-2sin^2x}\)
a) ĐK: \(\cos x\ne0\)( vì tan x = sinx/cosx nên cos x khác 0)
<=> \(x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
b) ĐK: \(1+\cos2x\ne0\Leftrightarrow\cos2x\ne-1\Leftrightarrow2x\ne\pi+k2\pi\Leftrightarrow x\ne\frac{\pi}{2}+k\pi\); k thuộc Z
=> TXĐ: \(ℝ\backslash\left\{\frac{\pi}{2}+k\pi\right\}\); k thuộc Z
c) ĐK: \(\hept{\begin{cases}\cot x-\sqrt{3}\ne0\\\sin x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne\frac{\pi}{6}+k\pi\text{}\text{}\\x\ne l\pi\end{cases}}\); k,l thuộc Z
=>TXĐ: ....
d) ĐK: \(1-2\sin^2x\ne0\Leftrightarrow\cos2x\ne0\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
=> TXĐ:...