Ai giúp tuôi zới ạk

Gấp

ÔK

DỂ QUÁ!!!!!!!!!!!!!!!!!!!!!!!!

tui hk biết làm

Mình học lớp 5 mà chưa học bài này

cô ra thêm bài khó trong giờ học cho mấy bạn giỏi có cái mà làm

\(AD=\frac{1}{3}\times CD\Rightarrow S_{ABF}=\frac{1}{3}\times S_{BFC}\)

\(BE=\frac{1}{3}\times AB\Rightarrow S_{BEF}=\frac{1}{3}\times S_{ABF}\)

\(\Rightarrow S_{BEF}=\frac{1}{3}\times\frac{1}{3}\times S_{BFC}=\frac{1}{9}\times S_{BFC}\Rightarrow S_{BEF}=\frac{1}{10}\times S_{BEC}\)

\(BE=\frac{1}{3}\times AB\Rightarrow S_{BEC}=\frac{1}{3}\times S_{ABC}\)

\(\Rightarrow S_{BEF}=\frac{1}{10}\times\frac{1}{3}\times S_{ABC}=\frac{1}{30}\times S_{ABC}\)

\(\Rightarrow S_{BAC}=30\times S_{BEF}=5400\left(cm^2\right)\)

hmmmm kia dọa tao à

Đéo Tin \(\sqrt{ }\)

a: AD=DB

=>S ADE=S BDE

b: S ABE=2/3*36=24cm²

=>S ADE=12cm²

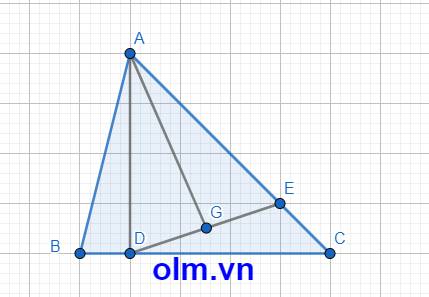
S_ADE = 2\(\times\)S_AGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )

⇒ S_ADE = 36 \(\times\) 2 = 72 (cm²)

S_ADE = \(\dfrac{3}{4}\)\(\times\)S_ADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)

⇒ S_ACD = 72 : \(\dfrac{3}{4}\) = 96 (cm²)

DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC

S_ADC = \(\dfrac{4}{5}\)S_ABC  (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)

⇒ S_ABC = 96 : \(\dfrac{4}{5}\) = 120 (cm²)

Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:

       72 : 120 = 0,6

       0,6 = 60%

Đáp số: 60% 

Xét ΔABC có \(\dfrac{AF}{AB}=\dfrac{2}{3}\)

nên \(S_{AFC}=\dfrac{2}{3}\cdot S_{ABC}=\dfrac{2}{3}\cdot18=12\left(cm^2\right)\)

Xét ΔAFC có \(\dfrac{AE}{AF}=\dfrac{AD}{AC}=\dfrac{1}{2}\)

nên ED//FC

Xét ΔAFC có ED//FC

nên \(\dfrac{ED}{FC}=\dfrac{AE}{AF}=\dfrac{1}{2}\)

Xét ΔAFC có ED//FC

nên ΔAED đồng dạng với ΔAFC

=>\(\dfrac{S_{AED}}{S_{AFC}}=\left(\dfrac{ED}{FC}\right)^2=\dfrac{1}{4}\)

=>\(S_{AED}=\dfrac{1}{4}\cdot S_{AFC}=3\left(cm^2\right)\)

\(S_{AED}+S_{EDCF}=S_{AFC}\)

=>\(S_{EDCF}=S_{AFC}-S_{AED}=9\left(cm^2\right)\)