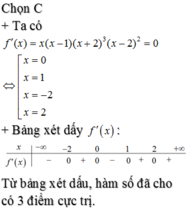Cho hàm số y=f(x) có đạo hàm f’(x)=x2(x-1)(x+2)3(2-x) ∀xϵR. Số điểm cực trị hàm số đã cho bằng

Những câu hỏi liên quan
Cho hàm số y=f(x) có đạo hàm f ’ ( x ) = x 2 ( x - 1 ) ( x + 2 ) 3 ( 2 - x ) . Số điểm cực trị của hàm số đã cho bằng
A. 7
B. 2
C. 4
D. 3
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x - 2 ) ( 3 x - 1 ) , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho bằng
A. 2
B. 1
C. 3
D. 4
Cho hàm số y=f(x) có đạo hàm f ’ ( x ) = x 2 ( x - 1 ) ( x 2 - 1 ) 3 . Số điểm cực trị của hàm số đã cho là
A. 2
B. 1
C. 8
D. 3
Chọn đáp án B
Phương pháp
Số điểm cực trị của hàm số y=f(x) là số nghiệm bội lẻ của phương trình f’(x)=0.
Cách giải
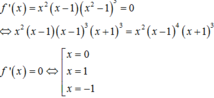
Tuy nhiên x=0 là nghiệm bội 2, x=1 là nghiệm bội 4 của phương trình f’(x)=0, do đó chúng không là cực trị của hàm số. Vậy hàm số có duy nhất 1 điểm cực trị x=-1.
Chú ý: HS nên phân tích đa thức f’(x) thành nhân tử triệt để trước khi xác định nghiệm, tránh sai lầm khi kết luận x=1 cũng là cực trị của hàm số.
Đúng 0
Bình luận (0)
Cho hàm số f(x) có đạo hàm
f
(
x
)
x
2
.
(
x
-
1
)
3
.
(
x
-
2
)
4
.
(
x
-...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' ( x ) = x 2 . ( x - 1 ) 3 . ( x - 2 ) 4 . ( x - 3 ) 5 ; ∀ x ∈ R . Số điểm cực trị của hàm số đã cho là:
A. 1
B. 4
C. 2
D. 3
Cho hàm số f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) 3 ( x - 2 ) 4 ( x - 3 ) 5 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 1
B. 4
C. 2
D. 3
Cho hàm số f(x) có đạo hàm
f
(
x
)
x
(
x
+
1
)
(
x
+
2
)
3
,
∀
x
∈
R
. Số điểm cực trị của hàm số
y
f
(
x
2
-
2
x
)
là A. 3. B. 2. C. 5. D. 4.
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' ( x ) = x ( x + 1 ) ( x + 2 ) 3 , ∀ x ∈ R . Số điểm cực trị của hàm số y = f ( x 2 - 2 x ) là
A. 3.
B. 2.
C. 5.
D. 4.
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x 2 - 1 ) ( x + 2 ) 3 , ∀ x ∈ ℝ . Hàm số có bao nhiêu điểm cực trị?
A. 3
B. 2
C. 5
D. 1
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) ( x 2 - 3 ) ( x 4 - 9 ) . Số điểm cực trị của hàm số y = f ( x ) là
A. 3
B. 4
C. 2
D. 1
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 3 ( x - 2 ) 2 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 4
B. 7
C. 3
D. 2
Cho hàm số y f(x) có đạo hàm f(x)
x
2
-
4
3
x
2
,
∀
x
≠
0
. Số điểm cực trị của hàm số đã cho là A. 3. B. 5. C. 2. D. 1.
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f'(x) = x 2 - 4 3 x 2 , ∀ x ≠ 0 . Số điểm cực trị của hàm số đã cho là
A. 3.
B. 5.
C. 2.
D. 1.
Chọn C
Ta có 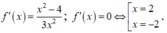
Nhận thấy f'(x) đổi dấu qua 2 nghiệm x = ± 2 nên hàm số y = f(x) có 2 điểm cực trị.
Đúng 0
Bình luận (0)