Cho tam giác ABC vuông tại A. Đường cao ah h gọi là điểm đối xứng h qua AC e là điểm đối xứng của H qua BC chứng minh rằng A là trung điểm của de

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC. Chứng minh rằng BC = BD + CE
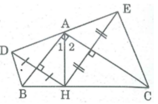
∆ ADB = ∆ AHB ⇒ BD = BH.
∆ AEC = ∆ AHC ⇒ CE = CH.
Vậy BD + CE = BH + CH = BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC. Chứng minh rằng D đối xứng với E qua A.
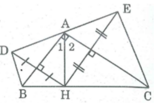
Điểm D đối xứng điểm H qua trục AB.
Suy ra AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực)
⇒ ∆ ADH cân tại A
Suy ra: AB là tia phân giác của ∠ (DAH)
⇒ ∠ (DAB) = ∠ A 1
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A
Suy ra: AC là đường phân giác của góc (HAE) ⇒ ∠ A 2 = ∠ (EAC)
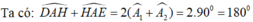
⇒ D, A, E thẳng hàng
Ta có: AD = AE (vì cùng bằng AH)
Suy ra điểm A là trung điểm của đoạn DE.
Vậy điểm D đối xứng với điểm E qua điểm A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC) có M là trung điểm BC. Gọi D là điểm đối xứng của A qua M. a) Chứng minh tứ giác ABCD là hình chữ nhật. b) Gọi AH là đường cao của tam giác ABC và K là điểm đối xứng với A qua H. Chứng minh rằng KD // BC, từ đó suy ra tứ giác BCDK là hình thang cân. c) Trên tia đối của tia CA lấy điểm E sao cho CE = CA. Chứng minh ba điểm K, D, E thẳng hàng
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại a đường cao AH Gọi H là trung điểm của AC lấy điểm Đ đối xứng với điểm H qua điểm I gọi e là trung điểm của AB Chứng Minh A đối xứng H qua EI
Cho tam giác ABC vuông góc tại đỉnh A. Kẻ đường cao AH. Gọi D,E theo thứ tự là các điểm đối xứng của điểm H qua AB,AC. Chứng minh rằng:
1. Điểm A là trung điểm của đoạn DE.
2. DE=2AH
1: Ta có: D và H đối xứng nhau qua AB
nên AB là đường trung trực của DH
Suy ra: AH=AD
Xét ΔAHD có AH=AD
nên ΔAHD cân tại A
mà AB là đường trung trực ứng với cạnh đáy HD
nên AB là tia phân giác của \(\widehat{HAD}\)
Ta có: H và E đối xứng nhau qua AC
nên AC là đường trung trực của HE
Suy ra: AE=AH
Xét ΔAEH có AE=AH
nên ΔAEH cân tại A
mà AC là đường trung trực ứng với cạnh đáy HE
nên AC là tia phân giác của \(\widehat{EAH}\)
Ta có: \(\widehat{DAE}=\widehat{EAC}+\widehat{HAC}+\widehat{HAB}+\widehat{DAB}\)
\(=2\cdot\left(\widehat{HAC}+\widehat{HAB}\right)\)
\(=2\cdot90^0=180^0\)
Suy ra: D,A,E thẳng hàng
mà AE=AD(=AH)
nên A là trung điểm của DH
2: Ta có: DE=AD+AE
nên DE=AH+AH
hay DE=2AH
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AI. M là điểm đối xứng với H qua AB, N là điểm đối xứng với H qua AC. D là giao điểm của MH với AB, E là giao điểm của NH với AC. Chứng minh rằng:
DE=AHM và N đối xứng nhau qua AAI vuông góc với DEHB.HC=AD.BD+AE.CECho tam giác ABC vuông tại A , AH là đường cao , góc ABC =60° . GỌI M LÀ TRUNG ĐIỂM CỦA AB , N LÀ TRUNG ĐIỂM CỦA AC . Lấy D đối xứng với H qua M và E đối xứng với H qua N. a, Chứng minh AH^2=AD. AE b, tia phân giác của góc ABC cắt AC tại K. Cm: sin góc ABC= 2sin góc ABK × cos CBK
Cho tam giác ABC vuông tại A, đường cao AH. D đối xứng với H qua AB. E đối xứng với H qua AC. Gọi I là giao điểm của AB và DH. K là giao điểm của AC và EH
a) Chứng minh AIHK là hình chữ nhật
b) Chứng minh D, E, A thẳng hàng
c) Gọi m là trung điểm của BC chứng minh AM vuông góc với IK
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng H qua AB. E là điểm đối xứng H qua AC. Gọi I là giao điểm của AD và BH. K là giao điểm của AC và EH.
a) Chứng minh: tứ giác ADHK là gì hình gì? Vì sao?
b) Chứng minh: 3 điểm D, E, A thẳng hàng
c) Gọi M là trung điểm của BC. Chứng minh AM vuông góc IK
(vẽ hình chứng minh giúp với) plz
Xem chi tiết












