CMR tam giác ABC vuông nếu : 3( cosB +2sinC ) + 4(sinB +2cosC) =15

Những câu hỏi liên quan
CMR tam giác ABC vuông nếu : 3( cosB +2sinC ) + 4( sinB +2cosC) =15
Cho tam giác ABC vuông tại A, đường cao AH. BIết BH=4cm, CH=9cm:
a/ Tính AB,AC,AH
b/ Cmr: 9.sinB+6.cosB-3.tanC=3√13 -2
c/ Gọi M,N lần lượt là hình chiếu của H trên AB,AC.
Cmr: AM.AN.BC=AH3
Cảm ơn nhiều nếu mn có câu trả lời!
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=HB\cdot HC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}\left(cm\right)\\AC=3\sqrt{13}\left(cm\right)\\AH=6\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có sinA+sinB= cosA+cosB. Chứng minh rằng tam giác ABC vuông.
1) ta co ket qua nhu sau:
sinAcosA+cosAcosB = sinAsinB+sinAcosA
<=> cosAcosB-sinAsinB=0
<=>cos(A+B)=0
<=> -cosC=0 (vi A+B+C=180)
hay cosC=0 => C=90
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A biết tanB=2. Tính \(\frac{sinB+cosB}{sinB-cosB}\)
Cho tam giác ABC vuông tại A, AB = 3 cm, AC = 4 cm. AH là đường cao. Hạ HK vuông góc AB, HI vuông góc AC. Tính
a) diện tích tứ giác AKHI
b) \(P=\frac{cosBsinC+2sin^2C-3cos^2B}{cosB+2sinC}\)
mik ko bít
I don't now
................................
.............
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A, có AC = (1/2).BC. Tính sinB, cosB, tgB, cotgB
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 ⇒ A B 2 = B C 2 - A C 2

Đúng 0
Bình luận (0)
Tam giác abc vuông tại a, có ac=1/2cb. Tính sinb, cosb, tanb, cotb.
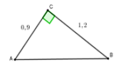
Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính các tỉ số lượng giác sinB và cosB.
A. sin B = 0,6; cos B = 0,8
B. sin B = 0,8; cos B = 0,6
C. sin B = 0,4; cos B = 0,8
D. sin B = 0,6; cos B = 0,4
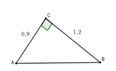
Theo định lý Py-ta-go ta có:
![]()
Xét tam giác ABC vuông tại C có:
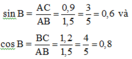
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại c có BC = 1,2 cm, AC = 0,9 cm . Tính các tỉ số lượng giác sinB; cosB
A. sinB = 0,6 cosB = 0,8
B. sinB = 0,8 cosB = 0,6
C. sinB = 0,4 cosB = 0,8
D. sinB = 0,6 cosB = 0,4