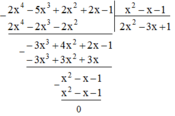thức hiện phép tính 1/99x97-1/97x95-1/95x93-...-1/5x3-1/3x1

Những câu hỏi liên quan
Thực hiện phép tính : 1/99x97 - 1/97x95 - 1/95x93 - ... - 1/5x3 - 1/3x1
Đặt A =\(\frac{1}{99x97}+\frac{1}{97x95}+...+\frac{1}{3x1}\)
2A =\(\frac{2}{99x97}+\frac{2}{97x95}+...+\frac{2}{3x1}\)
2A=\(\frac{1}{97}-\frac{1}{99}+\frac{1}{95}-\frac{1}{97}+...+\frac{1}{1}-\frac{1}{3}\)
2A=1-\(\frac{1}{99}\)=\(\frac{98}{99}\)
=> A=\(\frac{49}{99}\)
Đúng 0
Bình luận (0)
Tính
1/99x97 - 1/97x95-1/95x93-.........-1/5x3-1/3x1
1/99x97-1/97x95-1/95x93-1/5x3-1/3x1
1/99x97-1/97x95-1/95x93-....-1/5x3-1/3x1
Đặt \(A=\frac{1}{99.97}-\frac{1}{97.95}-\frac{1}{95.93}-....-\frac{1}{5.3}-\frac{1}{3.1}\)
\(\Rightarrow A=\frac{1}{99.97}-\left(\frac{1}{1.3}+\frac{1}{3.5}+....+\frac{1}{93.95}+\frac{1}{95.97}\right)\)
\(\Rightarrow A=\frac{1}{99.97}-\frac{1}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+....+\frac{1}{95}-\frac{1}{97}\right)\)
\(\Rightarrow A=\frac{1}{99}-\frac{1}{97}-\frac{1}{2}\left(1-\frac{1}{97}\right)=\frac{1}{99}-\frac{1}{97}-\frac{1}{2}-\frac{1}{194}\)
Đúng 0
Bình luận (0)
tính
1/99x97-1/97x95-1/95x93-....-1/3x1
\(\frac{1}{99x97}\)- \(\frac{1}{97x95}\) - \(\frac{1}{95x93}\) - \(\frac{1}{5x3}\) - \(\frac{1}{3x1}\)
\(\frac{-92}{93}\)
EM MỚI HỌK LỚP 6 THUI ẠK CHẮC K ĐÚNG HOẶC CÓ THỂ ĐÚNG ẠK NẾU ĐÚNG THÌ K ANH NHÓE!
CHÚC ANH HỌC TỐT
Đúng 1
Bình luận (0)
1/3x1 + 1/5x3 +.........+1/95x97+1/97x99
Đặt A=1/3x1 + 1/3x5 + ......+ 1/95x97 + 1/97x99
\(2A=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{97}-\frac{1}{99}\)
\(2A=1-\frac{1}{99}\)
\(A=\frac{98}{99}:2\)
\(A=\frac{49}{99}\)
Đúng 0
Bình luận (0)
a) Thực hiện phép chia đa thức (2x4 - 6x3 +12x2 - 14x + 3) cho đa thức (x2 – 4x +1)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)
Đúng 3
Bình luận (0)
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia:
2
x
2
-
5
x
3
+
2
x
+
2
x
4
-
1
:...
Đọc tiếp
Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi thực hiện phép chia: 2 x 2 - 5 x 3 + 2 x + 2 x 4 - 1 : x 2 - x - 1