Cho tam giác ABC. Vẽ phía ngoài tam giác ABC các tam giác vuông tại A là tam giác ABD và ACE có AB=AD, AC=AE. Kẻ AH vuông BC, DM vuông AH, EN vuông AH. Cmr:
a) DM=AH
b) MN đi qua trung điểm của DE
Cho tam giác Abc, vẽ phía ngoài tam giác ABC các tam giác vuông tại A là tam giác ABD;tam giác ACE; có AB =AD; AC=AE. kẻ AH vuông góc BC; DM vuông góc ANH; EN vuông góc AH. chứng minh: a) DM = AH; b) MN đi qua trung điểm DE
Cho tam giác ABC. Vẽ ở phía ngoài tam giác ABC các tam giác vuông tại A và ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng: MN đi qua trung điểm của DE
Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
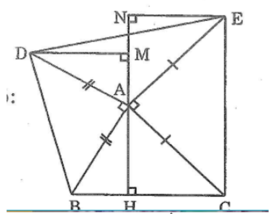
Cho tam giác ABC. Vẽ về phía ngoài tam giác ABC các tam giác vuông tại A là ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng :
a) DM = AH
b) MN đi qua trung điểm của DE
a) Ta có ˆBAH+ˆBAD+ˆDAM=180∘BAH^+BAD^+DAM^=180∘ (kề bù)
Mà ˆBAD=90∘⇒ˆBAH+ˆDAM=90∘BAD^=90∘⇒BAH^+DAM^=90∘ (1)
Trong tam giác vuông AMD, ta có:
ˆAMD=90∘⇒ˆDAM+ˆADM=90∘(2)AMD^=90∘⇒DAM^+ADM^=90∘(2)
Từ (1) và (2) suy ra: ˆBAH=ˆADMBAH^=ADM^
Xét hai tam giác vuông AMD và BHA, ta có:
ˆAMD=ˆBAH=90∘AMD^=BAH^=90∘
AB = AD (gt)
ˆBAH=ˆADMBAH^=ADM^ (chứng minh trên)
Suy ra: ∆AMD = ∆BHA (cạnh huyền, góc nhọn)
Vậy: AH = DM (2 cạnh tương ứng) (3)
b) Ta có: ˆHAC+ˆCAE+ˆEAN=180∘HAC^+CAE^+EAN^=180∘ (kề bù)
Mà ˆCAE=90∘(gt)⇒ˆHAC+ˆEAN=90∘CAE^=90∘(gt)⇒HAC^+EAN^=90∘ (4)
Trong tam giác vuông AHC, ta có:
ˆAHC=90∘⇒ˆHAC+ˆHCA=90∘(5)AHC^=90∘⇒HAC^+HCA^=90∘(5)
Từ (4) và (5) suy ra: ˆHCA=ˆEANHCA^=EAN^
Xét hai tam giác vuông AHC và ENA, ta có:
ˆAHC=ˆENA=90∘AHC^=ENA^=90∘
AC = AE (gt)
ˆHCA=ˆEANHCA^=EAN^ (chứng minh trên)
Suy ra: ∆AHC = ∆ENA (cạnh huyền, góc nhọn)
Vậy AH = EN (2 cạnh tương ứng)
Từ (3) và (6) suy ra : DM = EN
Vì DM⊥AHDM⊥AH và EN⊥AHEN⊥AH nên DM // EN (2 đường thẳng cùng vuông góc đường thẳng thứ 3)
Gọi O là giao điểm MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
ˆDMO=ˆENO=90∘DMO^=ENO^=90∘
DM = EN (chứng minh trên)
ˆMDO=ˆNEOMDO^=NEO^ (so le trong)
Suy ra: ∆DMO = ∆ENO (g.c.g) => OD = DE
Vậy MN đi qua trung điểm của DE.
Cho tam giác ABC. Vẽ về phía ngoài tam giác ABC các tam giác vuông tại A là ABD, ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng:
a) DM = AH.
b) MN đi qua trung điểm của DE.
Bạn tự vẽ hình nhé!
a, Có ∠BAH+ ∠BAD+ ∠DAM= 180 độ
=> ∠BAH+ ∠DAM= 180 độ- ∠BAD= 90 độ
Xét ΔDAM và ΔABH có
∠ DMA= ∠AHB = 90 độ
AD= AB
∠DAM= ∠ABH (vì cùng phụ với ∠BAH)
=> ΔDAM = ΔABH (ch-gn)
=> DM= AH
b, Có ∠HAC+ ∠EAC+ ∠NAE= 180 độ
=> ∠HAC+ ∠NAE= 180 độ- ∠EAC= 90 độ
Xét ΔEAN và ΔACH có
∠ ANE= ∠AHC = 90 độ
AE= AC
∠NAE= ∠ACH (vì cùng phụ với ∠HAC)
=> ΔEAN = ΔACH (ch-gn)
=> EN= AH
Mà DM= AH
=> EN= DM
c, Có EN ⊥ AH
DM ⊥ AH
=> EN // DM
=> ∠NEO= ∠ODM (2 góc so le trong)
Xét ΔDOM và ΔEON có
∠DMO = ∠ENO = 90 độ
DM= EN
∠ODM= ∠OEN(cmt)
=> ΔDOM = ΔEON (ch-gn)
=> OD = OD
=> O là trung điểm của DE
Bài tập) Cho tam giác ABC . Vẽ về phía ngoài tam giác ABC các tam giác tam giác vuông tại A là ABD,ACE có AB=AD , AC=AE .Kẻ AH vuông góc với BC ,DM vuông góc với AH ,EN vuông góc với AH .CMR :
a)DM=AH
b)MN đi qua trung điểm của DE
Cho tam giác ABC, vẽ về phía ngoài tam giác các tam giác vuong tại A là ABD và ACE, có AB=AD,AC=AE. VẼ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. CMR
A] DM=AH
B] MN đi qua trung điểm của DE
1) Vẽ hình..
2) Bài Làm
a, Ta có: BAHˆ+DAMˆ=90oBAH^+DAM^=90o;BAHˆ+ABHˆ=90oBAH^+ABH^=90o
⇒⇒DAMˆ=ABHˆDAM^=ABH^
Xét tam giác ADM vuông tại M và tam giác BAH vuông tại H ta có:
AD=BA(gt);DAMˆ=ABHˆDAM^=ABH^ (cmt)
Do đó tam giác ADM=tam giác BAH(cạnh huyền - góc nhọn)
=> DM=AH(cặp cạnh tương ứng) (đpcm)
b, Ta có: HACˆ+NAEˆ=90oHAC^+NAE^=90o;HACˆ+ACHˆ=90oHAC^+ACH^=90o
⇒⇒ NAEˆ=ACHˆNAE^=ACH^
Xét tam giác AEN vuông tại N và tam giác CAH vuông tại H ta có:
AE=CA(gt); NAEˆ=ACHˆNAE^=ACH^ (cmt)
Do đó tam giác AEN=tam giác CAH(cạnh huyền - góc nhọn)
=> EN=AH(cặp cạnh tương ứng)
mà DM=AH(cm câu a)
nên EN=DM
Gọi giao điểm của MN và DE là I (bạn tự thêm điểm trên hình nha mình quên)
Ta có: 90o−DIMˆ=90o−EINˆ→IDMˆ=IENˆ90o−DIM^=90o−EIN^→IDM^=IEN^
Xét tam giác DMI và tam giác ENI ta có:
DMIˆ=ENIˆ(=90o)DMI^=ENI^(=90o);DM=EN(đã cm);MDIˆ=NEIˆMDI^=NEI^(cmt)
Do đó tam giác DMI=tam giác ENI(g.c.g)
=> DI=EI(cặp cạnh tương ứng)
=> MN đi qua trung điểm của DE(đpcm)
Xét tam giác AND và BHA có:
DA = AB ( gt )
DNA = AHB ( = 90độ )
NDA=BAH(cùng phụ với DAN)
=>tam giác AND=BHA(ch-gn)
=>DN=AH nối A với E.giao diem giữa MNvà DE là O
vì DM VUÔNG GÓC AH EN VUÔNG GÓC AH =>DM song song
EN =>góc MEO=MDO XÉT TAM GIÁC MEA VÀ HAC CÓ
EA=AC
AME=AHC
MAE=ACH
=>TAM GIÁC MEA=HAC
=>ME=AH MÀ DM=AH
=>ME=DM
XÉT TAM GIÁC DNO VÀ EMO CÓ
DN=ME
DMN=ENM
EDM=NEO
=>TAM GIÁC DNO=NEO=>DO=OE
MN đi qua trung điểm DE
I) vẽ hình và viết giả thuyết, kết luận.
2) bài làm:
a) DM = AH
Ta có: \(\widehat{ABH}\) + \(\widehat{BAH}\) = 900 (vì tam giác AHB vuông tại H)
\(\widehat{DAM}\)+ \(\widehat{DAB}\)+ \(\widehat{BAH}\)= 1800
\(\Rightarrow\)\(\widehat{DAM}\)+ \(\widehat{BAH}\)= 1800 - \(\widehat{DAB}\)= 1800 - 900 = 900
Do đó: \(\widehat{ABH}\)= \(\widehat{DAM}\)( cùng phụ \(\widehat{BAH}\) )
Xét 2 tam giác vuông ABH và DAM có:
AB = AD ( gt)
\(\widehat{ABH}\)= \(\widehat{DAM}\)( chứng minh trên)
Suy ra: \(\Delta ABH\)= \(\Delta DAM\)( cạnh huyền- góc nhọn)
Vậy: DM = AH
b) MN đi qua trung điểm của DE
Gọi I là giao điểm của DE và MN
Xét 2 tam giác vuông ANE và CHA
Ta có: \(\widehat{NAE}=\widehat{HCA}\) ( Cùng phụ \(\widehat{HAC}\))
AE = AC ( gt)
Do đó: \(\Delta ANE=\Delta CHA\)( cạnh huyền- góc nhọn)
\(\Rightarrow\) NE = HA
mà: HA = DM 9 (chứng minh trên)
Nên: NE = DN
mặt khác: NE // DM ( cùng vuông góc với AH)
cho nên: \(\widehat{NEI}\)= \(\widehat{MDI}\)( Sole)
Xét 2 tam giác vuông MDI và NEI có:
NE = DN ( Chứng minh trên)
\(\widehat{NEI}\)= \(\widehat{MDI}\) ( Chứng minh trên )
\(\Rightarrow\) \(\Delta DMI\)= \(\Delta ENI\)( cạnh huyền - góc nhọn )
Nên: ID = IE
Vậy: MN đi qua trung điểm của DE
Cho tam giác ABC. Vẽ về phía ngoài của tam giác ABC các tam giác vuông tại A là ABD, ACE có AB= AD, AC=AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. CHứng minh rằng :
a) DM= AH
b) DM đi qua trung điểm của DE.
Cho tam giác ABC . Vẽ về phía ngoài tam giác ABC , các tam giác vuông tại A là ABD, ACE có AB = AD , AC = AE. Kẻ AH vuông với BC, DM vuông góc với AH, EN vuông góc với AH. chứng minh rằng :
a) DM = AH
b) MN đi qua trung ddiểm của DE
 a) Ta có :
a) Ta có :
Góc A2 + A3 + A1 = 189' ( bù nhau )
mà góc A3 = 90'
---> góc A2 + góc A1 = 180 - 90' = 90'
Vì góc DMA = góc AHB = 90'
--->góc D2 + góc A2 = 190' - góc DMA
--->góc D2 + góc A2 = 90'
---> góc A1 + góc B1 = 90'
--->góc D1 = góc A1; góc A2 = góc B1
xét hai tam giác vuông AMD và AHB có :
góc DMA = góc AHB ( vuông góc )
AD = AB ( GT )
góc A2 = góc B1 ( CMT )\
--->ΔDMA = ΔAHB ( cạnh huyền - góc nhọn )
---> DM = AH ( hai cạnh tương ứng)
b) Gọi M là giao điểm của MN và DE
Xét ΔANE và ΔCHA có :
( chứng minh như câu a)
---> EN = AH
Xét hai tam giác vuông IEN và IMD có :
góc I1 = góc I2 ( đối đỉnh )
EN = AH ( ΔANE = ΔCHA)
DM = AH ( CMT )
vì Tổng 3 góc tam giác = 180'
mà góc I1 = góc I2 ;
Góc M = góc N
---> ΔIMD = ΔENI ( cạnh huyền - góc nhọn)
---> DI = IE ( hai cạnh tương ứng 0
---> MN đi qua trung điểm của DE
cho tam giác ABC. Vẽ về phía ngoài tam giác ABC các tam giác vuông tại A là ABD, ACE, có AB=AD, AC=AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. CMR
a) DM=AH
b) MN là trung điểm của DE