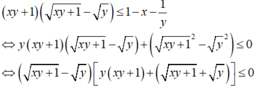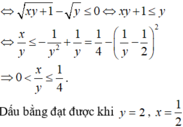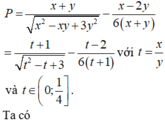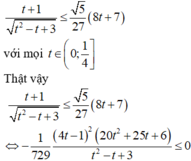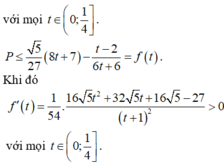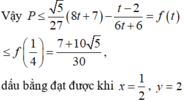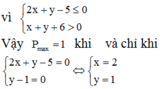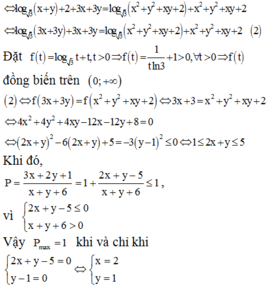tìm xy (x,y khác 0) sao xy - yx2 là SCP

Những câu hỏi liên quan
Tìm số nguyên tố có 2 chữ số khác nhau có dạng xy ( x > y > 0 ) sao cho hiệu của số đó với số viết theo thứ tự ngược lại của số đó là SCP
Theo bài ra ta có: xy - yx là số chính phương.
=> xy - yx = 10x + y -10 - y - x = 9.( x - y ) = 32.( x - y ) là số chính phương.
=> x - y là số chính phương.
Và x > y > 0
=> x - y = 1 hoặc x - y = 4.
Các số có 2 chữ số có chữ số hàng chục hơn hàng đơn vị 1 đơn vị:
10 ; 21 ; 32 ; 43 ; 54 ; 65 ; 76 ; 87 ; 98.
=> số cần tìm là 43.
Các số có 2 chữ số có chữ số hàng chục hơn hàng đơn vị 4 đơn vị:
40 ; 51 ; 62 ; 73 ; 84 ; 95.
=> số cần tìm là 73.
Vậy ta tìm được các số thõa mãn: 43 ; 73.
Đúng 1
Bình luận (1)
x- y=1 hoặc 4 vì x>y>0
=> Số chính phương chỉ có 1, 4, 9 là số chính phương có 1 chữ số.
Mà x>y>0 => chỉ có 1 và 4 thỏa mãn đề bài
Đúng 1
Bình luận (0)
Cho x,y là hai số thực dương thay đổi thỏa mãn điều kiện
(
x
y
+
1
)
(
x
y
+
1
-
y
)
≤
1
-
x
-
1
y
. Tìm giá trị lớn nhấ...
Đọc tiếp
Cho x,y là hai số thực dương thay đổi thỏa mãn điều kiện ( x y + 1 ) ( x y + 1 - y ) ≤ 1 - x - 1 y . Tìm giá trị lớn nhất của biểu thức P = x + y x 2 - x y + 3 y 2 - x - 2 y 6 ( x + y )
A. 5 3 - 7 30
B. 7 30 - 5 3
C. 5 3 + 7 30
D. 5 + 7 30
tìm x, y khác 0 sao cho ( x^2+1) chia hết cho ( xy- 1)tìm x, y khác 0 sao cho ( x^2+1) chia hết cho ( xy- 1)
bạn cho mình hỏi x,y có là số tự nhiên không
Rút gọn phân thức
x
2
−
xy
−
x
+
y
x
2
+
xy
−
x
−
y
ta được phân thức có mẫu là? A. x - y B.
x
−...
Đọc tiếp
Rút gọn phân thức x 2 − xy − x + y x 2 + xy − x − y ta được phân thức có mẫu là?
A. x - y
B. x − y x + y
C. x + y
D. (x - 1)(x + y)
Tìm hai số hữu tỉ x và y sao cho :
a) x+y =xy=x:y ( y khác 0)
b) x-y=xy=x:y( y khác 0)
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x(x - 3) + y(y - 3) + xy. Tìm giá trị Pmax của biểu thức P = 3 x + 2 y + 1 x + y + 6
A. Pmax = 0
B. Pmax = 2
C. Pmax = 1
D. Pmax = 3
Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
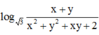
![]()
<=> ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
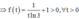
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
<=> ![]()
<=> ![]()
![]()
Khi đó, 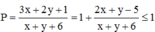
vì 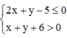
Vậy Pmax = 1 khi và chỉ khi 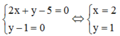
Đúng 0
Bình luận (0)
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
(
x
-
3
)
+...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y
Tìm giá trị P m a x của biểu thức P = 3 x + 2 y + 1 x + y + 6 .
![]()
![]()
![]()
![]()
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y . Tìm giá trị Pmax của biểu thức P = 3 x + 2 y + 1 x + y + 6
A. Pmax = 0
B. Pmax = 2
C. Pmax = 1
D. Pmax = 3
Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
Đặt ![]()
![]()
=> f(t) đồng biến trên (0;+∞)
![]()
![]()
![]()
![]()
![]()
Khi đó, 
vì 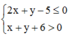
Vậy Pmax = 1 khi và chỉ khi 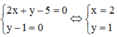
Đúng 0
Bình luận (0)
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) x y .
Tìm giá trị P m a x của biểu thức P = 3 x + 2 y + 1 x + y + 6 .
![]()
![]()
![]()
![]()